Συμβολομετρία
Η συμβολομετρία είναι μέθοδος που χρησιμοποιεί παρατηρήσεις της συμβολής υπερτιθέμενων κυμάτων για την εξαγωγή πληροφοριών σχετικώς με την πηγή ή τις πηγές των κυμάτων, μετά από υπολογισμούς.[1] Συνήθως εφαρμόζεται στα ηλεκτρομαγνητικά κύματα (όπως είναι και το φως), δια των οποίων αποτελεί σημαντική ερευνητική μέθοδο στα πεδία της αστρονομίας, της οπτικής των οπτικών ινών, της μετρολογίας, της ωκεανογραφίας, της σεισμολογίας, της φασματοσκοπίας (και των εφαρμογών της στη χημεία), της κβαντομηχανικής, της πυρηνικής και της σωματιδιακής φυσικής, της φυσικής πλάσματος, των βιομοριακών ενδοκυτταρικών αλληλεπιδράσεων, των διερευνήσεων επιφανειών, της μικρορευστομηχανικής, των μετρήσεων των μηχανικών καταπονήσεων, της ταχυμετρίας των ρευστών, της οπτομετρίας και της κατασκευής ολογραμμάτων.[2]:1–2
Τα συμβολόμετρα είναι οι συσκευές επί των οποίων βασίζεται η συμβολομετρία. Χρησιμοποιούνται ευρύτατα στην επιστήμη και τη βιομηχανία για τη μέτρηση μικροσκοπικών μετατοπίσεων, μεταβολών στον δείκτη διαθλάσεως και επιφανειακών ανωμαλιών. Στα περισσότερα συμβολόμετρα το φως από μία πήγη διαχωρίζεται σε δύο δέσμες που ακολουθούν διαφορετικές διαδρομές και κατόπιν συνδυάζονται και πάλι, δίνοντας το φαινόμενο της συμβολής. Δύο ασύμφωνες πηγές μπορούν επίσης να εμφανίσουν συμβολή κάτω από ορισμένες συνθήκες.[3] Οι παρατηρούμενοι κροσσοί συμβολής παρέχουν πληροφορίες σχετικώς με τη διαφορά των μηκών των διαδρομών του φωτός. Στην αναλυτική επιστήμη τα συμβολόμετρα χρησιμεύουν στη μέτρηση των μηκών και του σχήματος των οπτικών μερών με ακρίβεια νανόμετρου και θεωρούνται τα υψηλότερης ακρίβειας όργανα μετρήσεως μήκους που υπάρχουν. Στη φασματοσκοπία μετασχηματισμού Φουριέ, συμβολόμετρα αναλύουν το φως που περιλαμβάνει γραμμές απορροφήσεως ή εκπομπής μιας ουσίας ή μείγματος. Στην αστρονομία ένα συμβολόμετρο αποτελείται από δύο ή περισσότερα τηλεσκόπια ή ραδιοτηλεσκόπια τοποθετημένα σε κάποια απόσταση μεταξύ τους, τα οποία συνδυάζουν τα σήματα που λαμβάνουν προσφέροντας μια γωνιακή διακριτική ικανότητα ισοδύναμη με εκείνη που θα είχε ένα τηλεσκόπιο με διάμετρο ίση με τη μέγιστη απόσταση διαχωρισμού ανάμεσα στα τηλεσκόπια του συμβολόμετρου.
Βασικές αρχές
ΕπεξεργασίαΗ συμβολομετρία εφαρμόζει την αρχή της υπερθέσεως (ή αρχή της επαλληλίας) για να συνδυάζει κύματα με τρόπο τέτοιο ώστε το αποτέλεσμα να έχει κάποια χαρακτηριστικά διαγνωστικά της αρχικής καταστάσεως των κυμάτων. Κάθε φορά που συμβάλλουν δύο κύματα που έχουν την ίδια συχνότητα, το μοτίβο που προκύπτει καθορίζεται από τη διαφορά φάσεως ανάμεσα στα δύο κύματα: όπου τα κύματα συναντώνται με την ίδια φάση (συμφασικά), θα υπάρχει ενισχυτική συμβολή, ενώ όπου τα κύματα συναντώνται με μέγιστη διαφορά φάσεως θα έχουν αποσβεστική συμβολή. Στα σημεία όπου τα κύματα δεν είναι ούτε συμφασικά, ούτε με μέγιστη διαφορά φάσεως, θα υπάρχει ένα ενδιάμεσο μοτίβο εντάσεων, το οποίο μπορεί να χρησιμοποιηθεί για τον προσδιορισμό της σχετικής διαφοράς φάσεως. Τα περισσότερα συμβολόμετρα είναι κατασκευασμένα για να μετρούν τη συμβολή κυμάτων φωτός ή άλλων ηλεκτρομαγνητικών κυμάτων.[2]:3–12
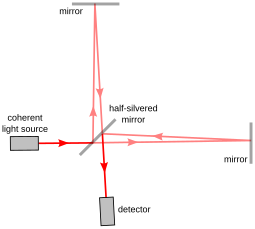
Συνήθως στη συμβολομετρία (δείτε την Εικόνα 1, τη διάταξη Μάικελσον) μία εισερχόμενη φωτεινή δέσμη σύμφωνου φωτός διαχωρίζεται σε δύο πανομοιότυπες δέσμες από έναν διαχωριστή δέσμης (π.χ. ένα ημιεπαργυρωμένο κάτοπτρο). Η καθεμιά από τις δύο δέσμες ακολουθεί μια διαφορετική διαδρομή και κατόπιν ξανασυναντώνται προτού φθάσουν σε έναν ανιχνευτή. Η διαφορά μεταξύ των δύο διαδρομών δημιουργεί μια διαφορά φάσεως ανάμεσα στις δύο δέσμες. Αυτή η διαφορά φάσεως δημιουργεί με τη σειρά της το σχέδιο κροσσών συμβολής[2]:14–17, που είναι ένα διαγνωστικό τού οτιδήποτε μεταβάλλει τη φάση κατά μήκος της κάθε διαδρομής. Αυτό θα μπορούσε να είναι μια διαφορά στο συνολικό μήκος της διαδρομής ή μια μεσολάβηση υλικού ή υλικών με διαφορετικό δείκτη διαθλάσεως κατά μήκος της μιας διαδρομής.[2]:93–103
Στις Εικόνες 2a και 2b ο παρατηρητής βλέπει απευθείας το κάτοπτρο M1 μέσα από τον διαχωριστή δέσμης, και ένα ανακλασμένο είδωλο M΄2 του κατόπτρου M2. Οι κροσσοί μπορούν να ερμηνευθούν ως αποτέλεσμα της συμβολής ανάμεσα στο φως που έρχεται από τα δύο φανταστικά είδωλα S΄1 και S΄2 της αρχικής πηγής φωτός S. Τα χαρακτηριστικά των σχημάτων που δημιουργεί η συμβολή εξαρτώνται από τη φύση της πηγής φωτός και από τον ακριβή προσανατολισμό των κατόπτρων και του διαχωριστή της δέσμης. Στην Εικόνα 2a τα οπτικά στοιχεία είναι προσανατολισμένα έτσι ώστε οι S΄1 και S΄2 να είναι ευθυγραμμισμένες με τον παρατηρητή και το προκύπτον σχήμα συμβολής αποτελείται από κύκλους με κέντρο την κάθετο στα κάτοπτρα M1 και M'2. Εάν, όπως στην Εικόνα 2b, τα M1 και M΄2 έχουν κλίση το ένα ως προς το άλλο, τότε οι κροσσοί συμβολής προσλαμβάνουν γενικώς το σχήμα κωνικών τομών (υπερβολών), ενώ εάν οι M΄1 και M΄2 αλληλοεπικαλύπτονται, οι κροσσοί κοντά στον άξονα θα είναι ευθύγραμμοι, παράλληλοι και ισαπέχοντες. Εάν η S είναι εκτεταμένη και όχι σημειακή πηγή φωτός, τότε οι κροσσοί συμβολής της Εικόνας 2a πρέπει να παρατηρηθούν με ένα τηλεσκόπιο εστιασμένο στο άπειρο, ενώ οι κροσσοί της Εικόνα 2b θα είναι εντοπισμένοι πάνω στα κάτοπτρα.[2]:17
Η χρήση λευκού φωτός δίνει ένα μοτίβο έγχρωμων κροσσών (Εικόνα 3).[2]:26 Ο κεντρικός κροσσός, που αντιπροσωπεύει διαδρομές ίσου μήκους, μπορεί να είναι φωτεινός ή σκοτεινός, αναλόγως του αριθμού των αντιστροφών φάσεως που υφίστανται οι δύο δέσμες κατά τη διαδρομή τους μέσα από το οπτικό σύστημα.[2]:26,171–172
Ιστορία
ΕπεξεργασίαΟι αρχές που διέπουν τη συμβολή του ορατού φωτός περιγράφηκαν για πρώτη φορά από τον Τόμας Γιανκ στη διάλεξη που έδωσε το 1803 στη Βασιλική Εταιρεία του Λονδίνου.[4] Ο Γιανγκ είχε εκτελέσει ένα πείραμα με διπλή σχισμή που έδειξε κροσσούς συμβολής. Η ερμηνεία του με βάση τη συμβολή των κυμάτων απορρίφθηκε από τους περισσότερους επιστήμονες της εποχής του εξαιτίας της κυριαρχίας της θεωρίας του Νεύτωνα ότι το φως αποτελείται από σωματίδια και όχι από κύματα.[5]
Ο Γάλλος μηχανικός Ωγκυστέν Φρενέλ, μη γνωρίζοντας το πείραμα του Γιανγκ, άρχισε να επεξεργάζεται μια κυματική θεωρία του φωτός και της συμβολής, οπότε τον σύστησαν στον Φρανσουά Αραγκό. Από το 1816 και μέχρι το 1818 οι Φρενέλ και Αραγκό πραγματοποίησαν πειράματα συμβολής στο Αστεροσκοπείο των Παρισίων. Εκείνο το χρονικό διάστημα ο Αραγκό σχεδίασε και κατασκεύασε το πρώτο συμβολόμετρο στην ιστορία, με το οποίο μέτρησε τον δείκτη διαθλάσεως του υγρού αέρα σε σχέση με τον ξηρό αέρα, ένα ζήτημα σχετιζόμενο με τις ακριβείς αστρονομικές παρατηρήσεις των θέσεων των αστέρων.[6] Η επιτυχία της κυματικής θεωρίας του φωτός του Φρενέλ εδραιώθηκε μετά το βραβευθέν υπόμνημά του το έτος 1819, με το οποίο ερμήνευε και μετρούσε τους κροσσούς συμβολής. Το συμβολόμετρο του Αραγκό χρησίμευσε αργότερα, το 1850, στον Λεόν Φουκώ για τη μέτρηση της ταχύτητας του φωτός στον αέρα σε σχέση με την ταχύτητά του στο νερό, καθώς και το 1851 στον Ιππόλυτο Φιζώ για τη μέτρηση της ταχύτητας του φωτός σε κινούμενο νερό σε σχέση με το ακίνητο.[7]
Ο Ζυλ Ζαμέν ανέπτυξε το πρώτο συμβολόμετρο μονής δέσμης το 1856. Αρκετά αργότερα, το 1881, ο Γερμανοαμερικανός φυσικός Άλμπερτ Α. Μάικελσον, ενώ βρισκόταν στο Βερολίνο για συζητήσεις με τον Χέρμαν φον Χέλμχολτς, επινόησε το συμβολόμετρο που φέρει το όνομά του, με σκοπό να ερευνήσει την επίδραση της κινήσεως της Γης στο διάστημα πάνω στην παρατηρούμενη ταχύτητα του φωτός. Το ότι δεν παρετήρησε καμιά τέτοια επίδραση, ούτε τότε ούτε αργότερα συνεργαζόμενος με τον Έντουαρντ Μόρλυ στο Οχάιο, αύξησε τις αμφιβολίες για την ύπαρξη ενός μέσου διαδόσεως του φωτός («αιθέρα»). Ο Αϊνστάιν είχε δηλώσει ότι ήδη η μέτρηση της ταχύτητας του φωτός σε κινούμενο νερό από τον Φιζώ με το συμβολόμετρο του Αραγκό τον οδήγησε στο να διατυπώσει τη θεωρία του για τη σχετικιστική άθροιση των ταχυτήτων.[8]
Κατηγορίες
ΕπεξεργασίαΤα συμβολόμετρα και οι συμβολομετρικές τεχνικές μπορούν να ταξινομηθούν με διαφορετικούς τρόπους:
Ομόδυνη και ετερόδυνη ανίχνευση
ΕπεξεργασίαΣτη λεγόμενη ομόδυνη ανίχνευση η συμβολή εκδηλώνεται με τη συνάντηση δύο δεσμών που έχουν το ίδιο μήκος κύματος (ή φέρουσα συχνότητα). Η διαφορά φάσεως ανάμεσα στις δύο δέσμες έχει ως αποτέλεσμα μια μεταβολή στην ένταση του κύματος στον ανιχνευτή. Μετρείται η προκύπτουσα ένταση μετά τη συγχώνευση των δύο δεσμών ή καταγράφεται/παρατηρείται το σχήμα των κροσσών συμβολής.[9] Τα περισσότερα συμβολόμετρα που περιγράφονται στο παρόν λήμμα εμπίπτουν στην κατηγορία αυτή.
Η ετερόδυνη ανίχνευση χρησιμοποιείται (1) για τη μετατόπιση ενός εισερχόμενου σήματος σε μια νέα περιοχή συχνοτήτων και (2) για την ενίσχυση ενός ασθενούς εισερχόμενου σήματος (με χρήση ενός ενεργού αναμείκτη). Ένα ασθενές εισερχόμενο σήμα που έχει συχνότητα f1 αναμειγνύεται με ένα ισχυρό σήμα με «συχνότητα αναφοράς» f2 από έναν τοπικό ταλαντωτή (LO). Ο μη γραμμικός συνδυασμός των δύο σημάτων δημιουργεί δύο νέα σήματα, το ένα με συχνότητα ίση με το άθροισμα f1 + f2 των δύο συχνοτήτων και το άλλο με συχνότητα ίση με τη διαφορά f1 − f2. Αυτές οι νέες συχνότητες ονομάζονται ετερόδυνες. Συνήθως χρειαζόμαστε τη μία από τις νέες συχνότητες, οπότε το άλλο σήμα αφαιρείται με ηλεκτρονικό φίλτρο. Το τελικό εξαγόμενο σήμα θα έχει ένταση ανάλογη του γινομένου των πλατών των εισερχόμενων σημάτων.[9]
Η σημαντικότερη και ευρύτερα χρησιμοποιούμενη εφαρμογή της ετερόδυνης τεχνικής είναι ο υπερετερόδυνος δέκτης (superhet), που εφευρέθηκε το 1917-1918 από τον Αμερικανό μηχανικό Έντγουιν Χάουαρντ Άρμστρονγκ και τον Γάλλο μηχανικό Λυσιέν Λεβύ. Στο κύκλωμα αυτό, το εισερχόμενο σήμα (από το ηλεκτρομαγνητικό κύμα που θέτει σε ταλάντωση τα ηλεκτρόνια μιας κεραίας) συμβάλλει με ένα σήμα από τοπικό ταλαντωτή (LO) και μετατρέπεται με την ετερόδυνη τεχνική σε σήμα μικρότερης σταθερής συχνότητας, που αποκαλείται ενδιάμεση συχνότητα (IF). Η IF ενισχύεται και «φιλτράρεται» προτού διοχετευθεί σε έναν ανιχνευτή (στην περίπτωση του ραδιοφώνου, ο ανιχευτής αυτός εξάγει το ηχητικό σήμα από το σήμα που του παρέχεται).[10]
Η οπτική ετερόδυνη ανίχνευση αποτελεί την εφαρμογή της ετερόδυνης τεχνικής στις συχνότητες του ορατού φωτός.[9]
Διπλή και κοινή διαδρομή
ΕπεξεργασίαΣυμβολόμετρο διπλής διαδρομής ή διπλού δρόμου αποκαλείται εκείνο στο οποίο η δέσμη αναφοράς και η δέσμη δείγματος ακολουθούν διαφορετικούς δρόμους. Τέτοια είναι το συμβολόμετρο του Μάικελσον, το συμβολόμετρο Twyman–Green και το συμβολόμετρο Mach–Zehnder. Μετά την αλληλεπίδραση με το υπό εξέταση δείγμα, η δέσμη δείγματος συμβάλλει με τη δέσμη αναφοράς, δημιουργώντας σχήματα συμβολής που μπορούν να ερμηνευθούν στη συνέχεια.[2]:13–22
Συμβολόμετρο κοινής διαδρομής ή κοινού δρόμου αποκαλείται εκείνο στο οποίο η δέσμη αναφοράς και η δέσμη δείγματος ακολουθούν την ίδια διαδρομή. Η Εικόνα 4 δείχνει το συμβολόμετρο Sagnac, το γυροσκόπιο οπτικής ίνας, το συμβολόμετρο σημειακής περιθλάσεως και το συμβολόμετρο πλευρικής μετατοπίσεως. Υπάρχουν και άλλα παραδείγματα συμβολομέτρων, όπως το μικροσκόπιο αντιθέσεως φάσεων Zernike, το δίπρισμα του Φρενέλ και το συμβολόμετρο πλάκας σκεδάσεως.[11]
Διαχωρισμός μετώπου κύματος και διαχωρισμός πλάτους
ΕπεξεργασίαΣυμβολόμετρα διαχωρισμού μετώπου κύματος
ΕπεξεργασίαΤο συμβολόμετρο διαχωρισμού μετώπου κύματος διαχωρίζει ένα μέτωπο κύματος που εξέρχεται από μια σημειακή οπή ή μια στενή σχισμή (χωρικώς σύμφωνο φως) και, αφού τα δύο μέρη του μετώπου διανύσουν διαφορετικές διαδρομές, συμβάλλουν.[12] Η Εικόνα 5 απεικονίζει το πείραμα συμβολής του Γιανγκ και το κάτοπτρο του Lloyd. Παραδείγματα συμβολομέτρων διαχωρισμού μετώπου κύματος είναι το δίπρισμα του Φρενέλ, ο διπλός φακός του Billet, το συμβολόμετρο Μάικελσον με φράγμα περιθλάσεως[13] και το συμβολόμετρο Rayleigh.[14]
Το 1803 το πείραμα συμβολής του Γιανγκ διεδραμάτισε μεγάλο ρόλο στη γενική αποδοχή της κυματικής θεωρίας του φωτός. Εάν το πείραμα γίνει με λευκό φως, τότε το αποτέλεσμα είναι μια λευκή κεντρική ζώνη συμβολής που αντιστοιχεί σε ίσο μήκος διαδρομής από τις δύο σχισμές, περιβαλλόμενη από ένα συμμετρικό σύνολο έγχρωμων κροσσών συμβολής με μειούμενη ένταση. Εκτός από τη συνεχή ηλεκτρομαγνητική ακτινοβολία, το πείραμα του Γιανγκ έχει διεξαχθεί με μεμονωμένα φωτόνια[15], με ηλεκτρόνια[16][17], ακόμα και με μόρια μπακμινστερφουλερενίου αρκετά μεγάλα ώστε να είναι ορατά με ηλεκτρονικό μικροσκόπιο.[18]
To κάτοπτρο του Lloyd δημιουργεί κροσσούς συμβολής από τη συνάντηση φωτός ερχόμενου κατευθείαν από μια πηγή (μπλε γραμμές) με φως από το ανακλώμενο είδωλο της πηγής (κόκκινες γραμμές) από ένα κάτοπτρο τοποθετημένο σε πολύ πλάγια γωνία. Το αποτέλεσμα είναι ένα ασύμμετρο «μοτίβο» κροσσών συμβολής. Η ζώνη ίσου μήκους διαδρομής, που είναι η εγγύτερη στο κάτοπτρο, είναι σκοτεινός και όχι φωτεινός κροσσός. Το 1834 ο Χάμφρυ Λόυντ ερμήνευσε αυτό το δεδομένο ως απόδειξη του ότι η φάση μιας επιφάνειας μετώπου κύματος που ανακλάται αντιστρέφεται.[19][20]
Συμβολόμετρα διαχωρισμού πλάτους
ΕπεξεργασίαΤο συμβολόμετρο διαχωρισμού πλάτους χρησιμοποιεί ένα ημιπερατό κάτοπτρο για να χωρίσει το πλάτος του του ξεχωριστές δέσμες, που κατόπιν ξαναενώνονται.
Το συμβολόμετρο Fizeau παρουσιάζεται στην Εικόνα 6 σε διάταξη ελέγχου ενός οπτικού επιπέδου (δηλαδή ενός γυαλιού που έχει λειανθεί με τη μέγιστη δυνατή ακρίβεια ώστε να έχει εντελώς επίπεδη επιφάνεια και χρησιμεύει για τη διαπίστωση της ακρίβειας της επιπεδότητας άλλων επιφανειών). Ένα εξίσου καλά λειασμένο οπτικό επίπεδο αναφοράς τοποθετείται πάνω από το ελεγχόμενο επίπεδο, διαχωριζόμενο από πολύ μικρά στηρίγματα. Το επίπεδο αναφοράς είναι ελαφρώς κεκλιμένο (μόνο ένα κλάσμα της μοίρας σε κλίση αρκεί), ώστε η πίσω επιφάνεια του επιπέδου να μη δίνει κροσσούς συμβολής. Ο διαχωρισμός των δύο επιπέδων (πλακών) επιτρέπει την κλίση αυτή. Ρυθμίζοντας την κλίση, που προσθέτει μια ελεγχόμενη βαθμίδα φάσεως στο σύστημα των κροσσών, μπορούμε να ελέγξουμε την απόσταση μεταξύ των κροσσών και τη διεύθυνση των κροσσών, έτσι ώστε να παραχθεί μια εύκολα ερμηνεύσιμη σειρά σχεδόν παράλληλων κροσσών αντί μια πολύπλοκη διάταξη περιγραμμάτων. Ωστόσο ο διαχωρισμός των πλακών υποχρεώνει στη ρύθμιση και εστίαση του φωτός. Η Εικόνα 6 δείχνει μια δέσμη μονοχρωματικού φωτός που φωτίζει τα δύο επίπεδα και έναν διαχωριστή δέσμης που επιτρέπει την παρατήρηση των κροσσών από τον άξονά τους.[21][22]
Το συμβολόμετρο Mach-Zehnder είναι ένα πιο ευέλικτο όργανο από το συμβολόμετρο Μάικελσον. Η καθεμιά από τις καλά διαχωρισμένες διαδρομές του φωτός διασχίζεται μόνο μία φορά και οι κροσσοί μπορούν να εστιασθούν πάνω σε οποιοδήποτε επιθυμητό επίπεδο.[2]:18 Συνήθως η συσκευή ρυθμίζεται έτσι ώστε οι κροσσοί να βρίσκονται στο ίδιο επίπεδο με το προς έλεγχο αντικείμενο, για να μπορούν να φωτογραφηθούν μαζί. Αν οι κροσσοί προκύπτουν από λευκό φως, τότε, επειδή το λευκό φως έχει περιορισμένο μήκος συμφωνίας, της τάξεως των μικρομέτρων, πρέπει να καταβάλλεται ιδιαίτερη φροντίδα να εξισώνονται οι οπτικές διαδρομές, αλλιώς δεν θα είναι ορατοί κροσσοί συμβολής. Καθώς φαίνεται στην Εικόνα 6, ένα εξισορροπητικό κελλί (compensating cell) τοποθετείται στη διαδρομή της δέσμης αναφοράς, ώστε να εξισορροπεί την καθυστέρηση της άλλης δέσμης από το κελλί ελέγχου. Οι ανακλαστικές επιφάνειες των διαχωριστών δέσμης προσανατολίζονται έτσι ώστε οι δύο δέσμες να διέρχονται από ίσο πάχος γυαλιού. Με τον προσανατολισμό αυτόν οι δύο δέσμες ανακλώνται από δύο φορές από εμπρόσθιες επιφάνειες, και επομένως η φάση της καθεμιάς έχει αντιστραφεί δύο φορές. Το αποτέλεσμα είναι ότι το φως που διανύει ίσες αποστάσεις και στις δύο δέσμες δημιουργεί έναν λευκό κροσσό ενισχυτικής συμβολής.[23][24]
Η καρδιά του συμβολομέτρου Fabry-Pérot είναι ένα ζεύγος από ημιεπαργυρωμένα γυάλινα οπτικά επίπεδα που απέχουν μεταξύ τους αρκετά χιλιοστά έως μερικά εκατοστά του μέτρου, με τις επαργυρωμένες επιφάνειες αντικρυστά η μία με την άλλη. (Εναλλακτικά, ένα etalon Fabry–Pérot διαθέτει μία διαφανή πλάκα (οπτικό επίπεδο) με δύο παράλληλες ανακλαστικές επιφάνειες.)[2]:35–36 Τα οπτικά επίπεδα, όπως και στο συμβολόμετρο Fizeau, έχουν μία ελαφρά κλίση. Σε ένα συνηθισμένο τέτοιο σύστημα, το φως παρέχεται από μια μη σημειακή διάχυτη πηγή, που βρίσκεται στο εστιακό επίπεδο ενός ρυθμιστικού φακού. Η εστίαση μέσω ενός άλλου φακού παράγει ό,τι θα ήταν ένα ανεστραμμένο είδωλο της πηγής εάν δεν υπήρχε το ζεύγος των οπτικών επιπέδων, δηλαδή χωρίς αυτά όλο το φως που εκπέμπεται από το σημείο A της πηγής και διέρχεται μέσα από το οπτικό σύστημα θα εστιαζόταν στο σημείο A΄. Στην Εικόνα 6 ιχνηλατείται μόνο μία ακτίνα που ξεκινά από το A. Καθώς η ακτίνα διέρχεται από το ζεύγος των οπτικών επιπέδων, ανακλάται πολλαπλώς, παράγοντας πολλαπλές ακτίνες που συλλέγονται από τον φακό εστιάσεως και καταλήγουν στο σημείο A΄ πάνω στην οθόνη. Το πλήρες σύστημα των κροσσών συμβολής λαμβάνει τη μορφή ενός συνόλου ομόκεντρων δακτυλίων. Η ευκρίνεια των δακτυλίων εξαρτάται από την ανακλαστικότητα των οπτικών επιπέδων. Εάν η ανακλαστικότητα είναι μεγάλη, οπότε ο παράγοντας Q είναι μεγάλος, το μονοχρωματικό φως δίνει ένα σύνολο στενών και φωτεινών δακτυλίων σε ένα σκούρο φόντο.[25] Στην Εικόνα 6 το μικρής ευκρίνειας είδωλο αντιστοιχεί σε μια ελάχιστη ανακλαστικότητα ίση με 0,04 (δηλαδή σε μη επαργυρωμένες επιφάνειες), ενώ το υψηλής ευκρίνειας είδωλο σε ανακλαστικότητα 0,95.
Η Εικόνα 6 δείχνει τα συμβολόμετρα Fizeau, Mach-Zehnder και Fabry-Pérot. Συμβολόμετρα διαχωρισμού πλάτους είναι επίσης το συμβολόμετρο Μάικελσον, το Twyman–Green, το συμβολόμετρο άνισης διαδρομής με λέιζερ και το συμβολόμετρο Linnik.[26]
Το Συμβολόμετρα Michelson-Morley
ΕπεξεργασίαΟι Μάικελσον και Μόρλυ (1887)[27], καθώς και άλλοι πειραματικοί της εποχής εκείνης πρωτοχρησιμοποίησαν τη συμβολομετρία σε μια προσπάθεια να προσδιορίσουν τις ιδιότητες του αιθέρα (του υποθετικού μέσου διαδόσεως του φωτός). Χρησιμοποιούσαν μονοχρωματικό φως μόνο για την αρχική ρύθμιση του εξοπλισμού τους, αλλά πάντοτε λευκό φως για τις ίδιες τις μετρήσεις του πειράματος. Ο λόγος ήταν ότι οι μετρήσεις καταγράφονταν με το μάτι. Το μονοχρωματικό φως θα έδινε ένα ομοιόμορφο μοτίβο κροσσών συμβολής. Επειδή δεν υπήρχαν τα σύγχρονα μέσα ρυθμίσεως της θερμοκρασίας, οι πειραματιστές είχαν να αντιμετωπίσουν τη συνεχή μετατόπιση των κροσσών από τις θερμοκρασιακές μεταβολές, ακόμα και αν το συμβολόμετρο ήταν εγκαταστημένο σε κάποιο υπόγειο. Επειδή επιπλέον οι κροσσοί θα εξαφανίζονταν πού και πού εξαιτίας δονήσεων από την οδική κυκλοφορία (τότε άμαξες με άλογα) και άλλους παράγοντες, θα ήταν εύκολο ο παρατηρητής να «χαθεί» όταν οι κροσσοί επανεμφανίζονταν. Συνεπώς το πλεονέκτημα του λευκού (σύνθετου) φωτός, το οποίο παρήγε ένα μοτίβο ξεχωριστών έγχρωμων κροσσών, υπερτερούσε των δυσκολιών στην ευθυγράμμιση της συσκευής εξαιτίας του μικρού μήκους συμφωνίας του.[28]
Εφαρμογές
ΕπεξεργασίαΦυσική και αστρονομία
ΕπεξεργασίαΣτη φυσική, ένα από τα σημαντικότερα πειράματα των τελών του 19ου αιώνα ήταν το περίφημο Πείραμα των Μάικελσον και Μόρλυ με το αρνητικό αποτέλεσμα, που παρέσχε υποστήριξη στην Ειδική θεωρία της σχετικότητας. Πρόσφατες επαναλήψεις του πειράματος αυτού βασίζονται σε ετερόδυνες μετρήσεις συχνοτήτων διακροτήματος διασταυρούμενων οπτικών κοιλοτήτων που ψύχονται σε πολύ χαμηλές θερμοκρασίες. Η Εικόνα 7 δείχνει ένα πείραμα με οπτική κοιλότητα που διεξάχθηκε από τους Müller κ.ά.[29] το 2003. Δύο οπτικές κοιλότητες κατασκευασμένες από κρύσταλλο σαπφείρου, που ελέγχουν τις συχνότητες δύο λέιζερ, είναι τοποθετημένες σε ορθές γωνίες μέσα σε έναν κρυοστάτη με υγρό ήλιο. Μια συσκευή συγκρίσεως συχνοτήτων μέτρησε τη συχνότητα διακροτήματος των συνδυασμένων ακτίνων εξόδου των δύο κοιλοτήτων. Μέχρι το 2010 η ακρίβεια με την οποία αποκλείσθηκε με αυτά τα πειράματα τυχόν ανισοτροπία στην ταχύτητα του φωτός είχε φθάσει[30][31] στην τάξη του 10−17.
| Εικόνα 7. Το πείραμα Michelson-Morley με ψυχόμενες οπτικές κοιλότητες. |
Εικόνα 8. Φασματοσκοπία μετασχηματισμού Φουριέ. |
Τα συμβολόμετρα Μάικελσον χρησιμοποιούνται εκτός του ομώνυμου πειράματος και σε ρυθμίσιμα οπτικά φίλτρα μικρού φασματικού εύρους[32], καθώς και ως η κυριότερη συνιστώσα των φασματόμετρων μετασχηματισμού Φουριέ.[33]
Στη χρήση τους ως ρυθμίσιμα φίλτρα μικρού φασματικού εύρους, τα συμβολόμετρα Μάικελσον έχουν πλεονεκτήματα και μειονεκτήματα σε σχέση με τεχνικές όπως αυτές των συμβολομέτρων Fabry-Pérot ή των φίλτρων Lyot. Τα συμβολόμετρα Μάικελσον έχουν το μεγαλύτερο εύρος πεδίου για συγκεκριμένο μήκος κύματος και η λειτουργία τους είναι σχετικώς απλή, καθώς η ρύθμισή τους γίνεται με μηχανική περιστροφή πλακών αντί με ηλεκτρικό έλεγχο πιεζοηλεκτρικών κρυστάλλων ή οπτικών ρυθμιστών νιοβιούχου λιθίου όπως σε ένα σύστημα Fabry-Pérot. Σε σύγκριση με τα φίλτρα Lyot, που έχουν διπλοθλαστικά στοιχεία, τα συμβολόμετρα Μάικελσον έχουν σχετικώς μικρή ευαισθησία στις θερμοκρασιακές μεταβολές. Από την άλλη, έχουν σχετικώς περιορισμένο εύρος μηκών κύματος και απαιτούν τη χρήση προ-φίλτρων, τα οποία όμως περιορίζουν τη διέλευση του φωτός.[34]
Η Εικόνα 8 δείχνει τη λειτουργία ενός φασματόμετρου μετασχηματισμού Φουριέ, το οποίο είναι ουσιαστικά ένα συμβολόμετρο Μάικελσον με το ένα κάτοπτρο να μπορεί να κινείται. Δημιουργεί ένα συμβολόγραμμα (αγγλ. interferogram) με τη λήψη μετρήσεων του σήματος σε πολλές διάκριτες τοποθετήσεις του κινούμενου κατόπτρου. Στη συνέχεια, ένας υπολογισμός με μετασχηματισμό Φουριέ μετατρέπει το συμβολόγραμμα σε ένα φάσμα.[35]
Etalons (συμβολόμετρα με συνενωμένα οπτικά στοιχεία) Fabry–Pérot με λεπτή επίστρωση χρησιμοποιούνται σε φίλτρα μικρού εύρους, που μπορούν να απεικονίζουν μία μεμονωμένη φασματική γραμμή. Για παράδειγμα, η γραμμή α του υδρογόνου ή η γραμμή K του ασβεστίου του ηλιακού ή του αστρικού φωτός.
Το Παρατηρητήριο Βαρυτικών κυμάτων Συμβολομέτρου Λέιζερ (LIGO) χρησιμοποιεί δύο συμβολόμετρα Michelson–Fabry–Pérot με διαδρομές φωτός μήκους 4 χιλιομέτρων για την ανίχνευση βαρυτικών κυμάτων.[36] Στην εφαρμογή αυτή η κοιλότητα Fabry-Pérot «αποθηκεύει» φωτόνια επί σχεδόν ένα χιλιοστό του δευτερολέπτου, ενώ αυτά αναπηδούν από το ένα κάτοπτρο στο άλλο. Αυξάνεται έτσι ο χρόνος στον οποίο ένα βαρυτικό κύμα μπορεί να αλληλεπιδράσει με τη συσκευή, με αποτέλεσμα πολύ καλύτερη ευαισθησία στις χαμηλές συχνότητες. Χρησιμοποιούνται επίσης μικρότερες κοιλότητες («mode cleaners») για χωρική διευκρίνηση και τη σταθεροποίηση συχνότητας του κύριου λέιζερ. Η πρώτη ανίχνευση βαρυτικών κυμάτων στην ιστορία έγινε από τα συμβολόμετρα του LIGO [37] στις 14 Σεπτεμβρίου 2015.
Ο ελευθέρως προσβάσιμος εσωτερικός χώρος του συμβολομέτρου Mach-Zehnder και η ευελιξία που προσφέρει για την παρατήρηση των κροσσών συμβολής το έχουν καταστήσει το προτιμώμενο συμβολόμετρο για την οπτικοποίηση της ροής σε ανεμοσήραγγες[38][39] και γενικότερα για μελέτες που περιλαμβάνουν οπτικοποίηση. Συχνές του χρήσεις γίνονται στην αεροδυναμική, στη φυσική πλάσματος και στη μεταφορά θερμότητας για τη μέτρηση πιέσεως, πυκνότητας και μεταβολών της θερμοκρασίας σε αέρια.[2]:18,93–95 Τα συμβολόμετρα Mach-Zehnder χρησιμεύουν επίσης στη μελέτη μιας από τις πλέον «αντιδιαισθητικές» προβλέψεις της κβαντομηχανικής, του φαινομένου που είναι γνωστό ως κβαντική διεμπλοκή.[40][41]
Στην αστρονομία η συμβολομετρία χρησιμεύει στην επίτευξη πολύ μεγάλων ισοδύναμων μεγεθύνσεων (διακριτικών ικανοτήτων) σε παρατηρήσεις, χάρη στην τεχνική της συνθέσεως διαμετρήματος, με τη συνδυασμένη μελέτη σημάτων από μια διάταξη επακριβώς τοποθετημένων σχετικώς μικρών τηλεσκοπίων αντί από ένα και μόνο, κατά πολύ ακριβότερο τηλεσκόπιο.[42]
Ιστορικώς η αστρονομική συμβολομετρία ξεκίνησε και ακόμη κυρίως επικεντρώνεται στη ραδιοαστρονομία: Διατάξεις ραδιοτηλεσκοπίων όπως η VLA αποτελούνται από τέτοια όργανα τοποθετημένα σε μια διάταξη στο έδαφος. Ωστόσο η κάλυψη γραμμών βάσεως παρέμενε ανεπαρκής. Η αδυναμία αυτή αντιμετωπίσθηκε με εκμετάλλευση της περιστροφής της Γης, που προκαλεί και την περιστροφή των ραδιοτηλεσκοπίων σε σχέση με τα ουράνια σώματα. Επιτεύχθηκαν έτσι γραμμές βάσεως με μήκος χιλιάδων χιλιομέτρων, η λεγόμενη συμβολομετρία πολύ μεγάλης γραμμής βάσης.[42]
Η οπτική αστρονομική συμβολομετρία (στο ορατό και το υπέρυθρο φως) χρειάσθηκε να υπερνικήσει δύσκολα τεχνικά ζητήματα. Το πολύ μικρό μήκος των κυμάτων του φωτός καθιστά απαραίτητη την απόλυτη ακρίβεια και σταθερότητα κατασκευής των συμμετεχόντων τηλεσκοπίων, ώστε η θέση τους να είναι γνωστή με ακρίβεια συγκρίσιμη με το μήκος αυτό, περίπου μισό εκατομμυριοστό του μέτρου. Σε αυτό το μήκος κύματος, διακριτική ικανότητα 1 χιλιοστού του δευτερολέπτου της μοίρας απαιτεί τηλεσκόπια που απέχουν μεταξύ τους 100 μέτρα. Οι συμβολομετρικές μετρήσεις απαιτούν αντίστοιχα υψηλή ευαισθησία και ανιχνευτές ακριβείας που έγιναν διαθέσιμοι μόλις στα τέλη του 20ού αιώνα. Η ατμοσφαιρική τύρβη, που προκαλεί και το «τρεμόσβημα» των άστρων, εισάγει ταχείες και τυχαίες μεταβολές στη φάση του εισερχόμενου φωτός, και επομένως απαιτεί data collection rates to be faster than the rate of turbulence.[44][45] Παρά τις τεχνικές αυτές δυσχέρειες, τρείς μείζονες εγκαταστάσεις λειτουργούν σήμερα, προσφέροντας διακριτική ικανότητα της τάξεως του κλάσματος του χιλιοστού του δευτερολέπτου της μοίρας: η CHARA στο Αστεροσκοπείο του όρους Γουίλσον, το NPOI στην Αριζόνα και το Πολύ Μεγάλο Τηλεσκόπιο (VLT) στη Χιλή στη συμβολομετρική του λειτουργία.
Ο κυματοσωματιδιακός δυϊσμός στην πλευρά του κυματικού χαρακτήρα της ύλης δίνει τη δυνατότητα κατασκευής συμβολομέτρων που να βασίζονται σε σωματίδια ύλης αντί για ηλεκτρομαγνητικά κύματα. Τέτοια παραδείγματα ήταν τα συμβολόμετρα ηλεκτρονίων και αργότερα τα συμβολόμετρα νετρονίων. Περί το 1990 λειτούργησαν τα πρώτα συμβολόμετρα ατόμων και ακολούθησαν συμβολόμετρα που χρησιμοποιούσαν ολόκληρα μόρια.[46][47][48]
Η ολογραφία ηλεκτρονίων είναι μια απεικονιστική τεχνική που καταγράφει το μοτίβο της συμβολής ηλεκτρονίων ενός αντικειμένου, το οποίο μετά ανακατασκευάζεται προκειμένου να δώσει μια πολύ μεγεθυμένη εικόνα του αντικειμένου.[49] Η τεχνική αναπτύχθηκε για την επίτευξη μεγαλύτερων μεγεθύνσεων στην ηλεκτρονική μικροσκοπία, καθώς το διακριτικό όριο της συμβατικής ηλεκτρονικής μικροσκοπίας δεν το καθορίζει το μήκος κύματος της δέσμης ηλεκτρονίων, αλλά οι μεγάλες συγκριτικώς ατέλειες των ηλεκτρονιακών φακών.[50]
Η συμβολομετρία νετρονίων έχει χρησιμοποιηθεί για τη διερεύνηση του φαινομένου Aharonov-Bohm, για την εξέταση της επιδράσεως της βαρύτητας πάνω σε ένα στοιχειώδες σωμάτιο, καθώς και για την επίδειξη μιας παράδοξης συμπεριφοράς των φερμιονίων που ερμηνεύεται με την απαγορευτική αρχή του Πάουλι: Αντίθετα με τα μακροσκοπικά σώματα, όταν τα φερμιόνια περιστρέφονται κατά 360° γύρω από οποιονδήποτε άξονα δεν βρίσκονται ξανά στην αρχική τους κατάσταση, αλλά η κυματοσυνάρτησή τους αποκτά αρνητικό πρόσημο. Με άλλα λόγια, ένα φερμιόνιο χρειάζεται να περιστραφεί κατά 720° προτού επιστρέψει στην αρχική του κατάσταση.[51]
Σήμερα οι τεχνικές της συμβολομετρίας ατόμων φθάνουν σε αρκετή ακρίβεια ώστε να επιτρέπουν εργαστηριακής κλίμακας ελέγχους της Γενικής θεωρίας της σχετικότητας.[52]
Συμβολόμετρα χρησιμοποιούνται στη φυσική της ατμόσφαιρας για υψηλής ακριβείας μετρήσεις αερίων που βρίσκονται σε ίχνη στον αέρα. Υπάρχουν αρκετά παραδείγματα, τόσο με μετρήσεις από γραμμές απορροφήσεως, όσο και με μετρήσεις από γραμμές εκπομπής. Μια συνήθης χρήση είναι η συνεχής παρακολούθηση της συγκεντρώσεως (σε μια στήλη της ατμόσφαιρας πάνω από το όργανο) αερίων όπως το όζον και το μονοξείδιο του άνθρακα.[53]
Μηχανική και εφαρμοσμένη επιστήμη
ΕπεξεργασίαΗ συμβολομετρία με δοκιμαστική πλάκα χρησιμεύει συχνά στην οπτική βιομηχανία για τον έλεγχο της ποιότητας επιφανειών κατά τη διαμόρφωση του σχήματός τους. Εικόνα 10 δείχνει φωτογραφίες οπτικών επιπέδων αναφοράς που χρησιμοποιούνται για τον έλεγχο δύο δοκιμαστικών οπτικών επιπέδων σε διάφορα στάδια της κατασκευής τους. Διακρ[νονται τα διαφορετικά μοτίβα των κροσσών συμβολής. Τα επίπεδα αναφοράς βρίσκονται με τις κάτω επιφάνειές τους σε επαφή με τα δοκιμαστικά και φωτίζονται από μονοχρωματική πηγή φωτός. Τα κύματα του φωτός που ανακλώνται από τις δύο επιφάνειες συμβάλλουν, δημιουργώντας ένα σύνολο από φωτεινές και σκοτεινές ζώνες. Η επιφάνεια στα αριστερά είναι σχεδόν επίπεδη και δίνει ένα μοτίβο από ευθύγραμμους, παράλληλους και ισαπέχοντες μεταξύ τους κροσσούς συμβολής. Η επιφάνεια στα δεξιά είναι καμπυλόγραμμη και δίνει ένα μοτίβο καμπυλόγραμμων κροσσών. Το κάθε ζεύγος γειτονικών μεταξύ τους κροσσών αντιπροσωπεύει διαφορά ύψους επιφάνειας ίση με το μισό του μήκους κύματος του φωτός που χρησιμοποιείται, οπότε οι διαφορές στο πάχος του οπτικού στοιχείου μπορούν να μετρηθούν απαριθμώντας τους κροσσούς. Το κατά πόσο οι επιφάνειες είναι επίπεδες μπορεί να μετρηθεί με ακρίβεια 50 δισεκατομμυριοστών του μέτρου με τη μέθοδο αυτή. Προκειμένου να διαπιστωθεί εάν η επιφάνεια υπό έλεγχο είναι κοίλη ή κυρτή ως προς το οπτικό επίπεδο αναφοράς, υπάρχουν διάφορες τεχνικές: μπορεί να παρατηρηθεί η μετατόπιση των κροσσών όταν πιεσθεί ελαφρώς το επάνω οπτικό επίπεδο. Αν εξετασθούν οι κροσσοί τους οποίους δίνει το λευκό (σύνθετο) φως, τότε η ακολουθία των χρωμάτων γίνεται οικεία με την εμπειρία και βοηθεί στην ερμηνεία των κροσσών. Μπορεί επίσης να συγκριθεί η εμφάνιση των κροσσών καθώς αυτοί παρατηρούνται από διαφορετικές γωνίες.[54]
Τα etalons Fabry-Pérot χρησιμοποιούνται ευρύτατα στις τηλεπικοινωνίες, τα λέιζερ και τη φασματοσκοπία για τον έλεγχο και τη μέτρηση των μηκών κύματος του φωτός. Τα διχρωικά φίλτρα είναι etalons πολλαπλών λεπτών στρωμάτων. Στις τηλεπικοινωνίες η πολυπλεξία μερισμού μήκους κύματος, η τεχνική που καθιστά ικανή τη χρήση πολλών διαφορετικών μηκών κύματος φωτός σε μία και μόνη οπτική ίνα, εξαρτάται από δομές φίλτρων που είναι etalons λεπτών στρωμάτων. Σε λέιζερ τα etalons χρησιμεύουν στον αποκλεισμό όλων των άλλων τρόπων ταλαντώσεως των φωτονίων στη συγκεκριμένη οπτική κοιλότητα, εκτός από τον μοναδικό που έχει επιλεγεί (single-mode lasers).[2]:42
Το συμβολομετρία Twyman-Green, που επινοήθηκε από τους Twyman και Green το 1916, είναι μια παραλλαγή του συμβολομέτρου Μάικελσον που χρησιμοποιείται ευρύτατα για τον έλεγχο οπτικών στοιχείων.[55] Διαφέρει από το Μάικελσον στο ότι χρησιμοποιεί μονοχρωματική και σημειακή πηγή φωτός, καθώς και έναν ρυθμιστή εστιάσεως. Ο ίδιος ο Μάικελσον, το 1918, επέκρινε τον σχεδιασμό των Twyman και Green ως ακατάλληλο για τον έλεγχο μεγάλων οπτικών στοιχείων, καθώς οι πηγές φωτός που ήταν τότε διαθέσιμες είχαν περιορισμένο μήκος συμφωνίας. Ο Μάικελσον υπεστήριξε ότι οι γεωμετρικοί περιορισμοί που επέβαλε το περιορισμένο μήκος συμφωνίας απαιτούσαν τη χρήση κατόπτρου αναφοράς με τις ίδιες διαστάσεις με το κάτοπτρο ελέγχου, κάτι που καθιστούσε το Twyman-Green μη πρακτικό για πολλές εφαρμογές.[56] Δεκαετίες αργότερα, η χρήση των λέιζερ αναίρεσε τις αντιρρήσεις του Μάικελσον.
Τα συμβολόμετρα Mach-Zehnder βρίσκουν εφαρμογή σε ολοκληρωμένα οπτικά κυκλώματα, στα οποία συμβάλλει το φως από δύο κλάδους ενός κυματοδηγού που ρυθμίζονται εξωγενώς ώστε η σχετική τους φάση να μεταβάλλεται. Μια ελαφρά κλίση του ενός από τους διαχωριστές δέσμης έχει ως αποτέλεσμα μια διαφορά στο μήκος της διαδρομής και άρα μια μεταβολή στο μοτίβο των κροσσών συμβολής. Τα συμβολόμετρα Mach-Zehnder αποτελούν τη βάση μιας ευρείας ποικιλίας συσκευών, από διαμορφωτές RF μέχρι αισθητήρες[57][58] και οπτικούς διακόπτες.[59]
Τα προταθέντα γιγαντιαία αστρονομικά τηλεσκόπια, όπως το Τηλεσκόπιο των τριάντα μέτρων και το Εξαιρετικά Μεγάλο Τηλεσκόπιο, θα έχουν κύρια κάτοπτρα αποτελούμενα από εκατοντάδες εξαγωνικά τμήματα. Η λείανση και η διαμόρφωση αυτών των ασύμμετρων τμημάτων είναι μια μεγάλη τεχνολογική πρόκληση. Παραδοσιακά, το ακριβές σχήμα τους ελεγχόταν με τη σύγκριση των (μη σφαιρικών) επιφανειών τους με μία σφαιρική επιφάνεια αναφοράς, με τη βοήθεια του λεγόμενου «μηδενικού διορθωτή» (null corrector). Από τη δεκαετία του 2010, ολογράμματα δημιουργούμενα από υπολογιστή (CGH) έχουν αρχίσει να αντικαθιστούν τους μηδενικούς διορθωτές με τη βοήθεια συμβολομέτρων Fizeau.[60]
Το γυροσκόπιο λέιζερ δακτυλίου (RLG) και το γυροσκόπιο οπτικής ίνας (FOG) είναι συμβολόμετρα χρησιμοποιούμενα σε συστήματα πλοηγήσεως και λειτουργούν με βάση την αρχή του φαινομένου Sagnac. Η διαφορά μεταξύ RLG και FOG είναι ότι στο RLG ολόκληρος ο δακτύλιος αποτελεί τμήμα του λέιζερ, ενώ στο FOG ένα εξωτερικό λέιζερ εισάγει δύο δέσμες που διαδίδονται αντίθετα η μία ως προς την άλλη μέσα σε έναν δακτύλιο από Οπτική ίνα, οπότε η περιστροφή του συστήματος προκαλεί μια μετατόπιση φάσεως ανάμεσα στις δύο δέσμες. Σε ένα RLG η παρατηρούμενη μετατόπιση φάσεως είναι ανάλογη προς τη συσσωρευμένη γωνία περιστροφής, ενώ σε ένα FOG η παρατηρούμενη μετατόπιση φάσεως είναι ανάλογη προς τη γωνιακή ταχύτητα[61]
Στα τηλεπικοινωνιακά δίκτυα η ετεροδύνωση διοχετεύει συχνότητες μεμονωμένων σημάτων σε διαφορετικά κανάλια, που μπορεί να έχουν κοινή μία μόνο υλική γραμμή μεταδόσεως. Αυτό αποκαλείται πολυπλεξία μερισμού συχνότητας (FDM). Π.χ. ένα ομοαξονικό καλώδιο ενός συστήματος καλωδιακής τηλεοράσεως μπορεί να μεταφέρει 500 τηλεοπτικά κανάλια ταυτοχρόνως, επειδή στο καθένα έχει εκχωρηθεί μία διαφορετική συχνότητα, έτσι ώστε να μη παρεμβάλλονται το ένα στο άλλο. Οι ανιχνευτές συνεχών κυμάτων (CW) των ραντάρ ντόπλερ είναι κατά βάση συσκευές ετερόδυνης ανιχνεύσεως που συγκρίνουν την εκπεμπόμενη με την ανακλώμενη δέσμη.[62]
Η ετερόδυνη ανίχνευση φωτός χρησιμοποιείται για σύμφωνες μετρήσεις με ντόπλερ LIDAR, ικανές να ανιχνεύουν πολύ ασθενή φωτεινά σήματα που σκεδάζονται από την ατμόσφαιρα και να καταγράφουν τις ταχύτητες του ανέμου με εξαιρετική ακρίβεια. Επίσης έχει εφαρμογές στις τηλεπικοινωνίες οπτικών ινών, σε διάφορες φασματοσκοπικές τεχνικές υψηλής αναλύσεως, ενώ η «αυτοετερόδυνη» μέθοδος μπορεί να χρησιμοποιηθεί στη μέτρηση του φασματικού εύρους του φωτός ενός λέιζερ.[9][63]
Η οπτική ετερόδυνη ανίχνευση ειναι πολύ χρήσιμη στις υψηλής ακρίβειας μετρήσεις των συχνοτήτων πηγών φωτός, καθώς και στη σταθεροποίηση των συχνοτήτων τους. Μέχρι και τη δεκαετία του 2010, μακρές «αλυσίδες συχνοτήτων» απαιτούνταν για να συνδεθεί η συχνότητα μικροκυμάτων της πηγής ενός ατομικού ρολογιού με συχνότητες κυμάτων φωτός. Σε κάθε κρίκο της αλυσίδας χρειαζόταν ένας πολλαπλασιαστής συχνότητας για να δώσει μια αρμονική της συχνότητας του συγκεκριμένου βήματος, η οποία συγκρινόταν με ετερόδυνη ανίχνευση με το επόμενο βήμα. Η κάθε μέτρηση μιας και μόνης φασματικής γραμμής απαιτούσε χρόνια προσπαθειών για την κατασκευή μιας «επί τούτου» αλυσίδας συχνοτήτων. Σήμερα οπτικές «χτένες συχνοτήτων» έχουν παράσχει μια πολύ απλούστερη μέθοδο μετρήσεως συχνοτήτων για τα κύματα φωτός. Εάν ένα παλμικό λέιζερ ρυθμισθεί ώστε να εκτοξεύσει έναν συρμό παλμών διάρκειας τρισεκατομμυριοστών του δευτερολέπτου, τότε το φάσμα του παρατηρείται να αποτελείται από τη «φέρουσα συχνότητα» περιβαλλόμενη από μια «χτένα» παράπλευρων συχνοτήτων με μικρά διαστήματα μεταξύ τους ίσα με τη συχνότητα επαναλήψεως του παλμού. Η συχνότητα αυτή «κλειδώνεται» με εκείνη της πρότυπης συχνότητας και οι μικρότερες από τις συχνότητες της «χτένας» διπλασιάζονται και ετεροδύνονται με εκείνες στο άλλο άκρο της χτένας. Η χτένα έτσι εξυπηρετεί ως αυτοαναφορά. Με τον τρόπο αυτόν, το «κλείδωμα» της συχνότητάς της σε ένα ατομικό πρότυπο μπορεί να γίνει με ένα και μοναδικό βήμα. Για τη μέτρηση τώρα μιας άγνωστης συχνότητας, το εξαγόμενο της χτένας αναλύεται σε ένα φάσμα, η άγνωστη συχνότητα ταυτίζεται με το κατάλληλο στοιχειώδες τμήμα από το φάσμα αυτό και μετρείται με ετερόδυνο κύκλωμα η συχνότητα διακροτήματος.[64][65]
Από τις συνηθέστερες βιομηχανικές εφαρμογές της οπτικής συμβολομετρίας είναι ως ευέλικτου εργαλείου μετρήσεων για την υψηλής ακριβείας εξέταση των ανωμαλιών μιας επιφάνειας. Κοινές τεχνικές συμβολομετρικών μετρήσεων είναι μεταξύ άλλων η Συμβολομετρία Μετατοπίσεως Φάσεων (Phase Shifting Interferometry, PSI)[66] και η Συμβολομετρία Κάθετης Σάρωσης (Vertical Scanning Interferometry, VSI)[67], γνωστή και ως «συμβολομετρία σαρώσεως λευκού φωτός» (SWLI) και με τον όρο ISO «συμβολομετρία σαρώσεως συμφωνίας» (CSI)[68]. Η CSI εκμεταλλεύεται τη συμφωνία προκειμένου να επεκτείνει τις δυνατότητες της συμβολομετρικής μικροσκοπίας.[69][70] Αυτές οι τεχνικές εφαρμόζονται ευρύτατα στην κατασκευή μικροηλεκτρονικών και μικροοπτικών στοιχείων. Η PSI γίνεται με μονοχρωματικό φως και δίνει πολύ ακριβείς μετρήσεις. Ωστόσο μπορεί να χρησιμεύσει μόνο για πολύ λείες επιφάνειες. Η CSI γίνεται συχνά με λευκό φως και αντί να καταγράφει τη φάση των κροσσών όπως η PSI, αναζητεί την καλύτερη θέση της μέγιστης αντιθέσεως φωτός και σκότους στους κροσσούς, ή κάποιο άλλο χαρακτηριστικό του συνολικού «μοτίβου» των κροσσών. Στην απλούστερη μορφή της η CSI παρέχει λιγότερο ακριβείς μετρήσεις από ό,τι η PSI, αλλά μπορεί να εφαρμοσθεί σε πιο ακανόνιστες επιφάνειες. Κάποια είδη της CSI, γνωστά με διάφορες ονομασίες όπως «Ενισχυμένη VSI» (EVSI), «SWLI υψηλής αναλύσεως» ή «Ανάλυση Χώρου Συχνοτήτων» (FDA), εκμεταλλεύονται φαινόμενα της συμφωνίας σε συνδυασμό με τη φάση συμβολής προκειμένου να ενισχύσουν την ακρίβεια.[71][72]
Η PSI επιλύει αρκετά ζητήματα σχετικώς με την κλασική ανάλυση στατικών συμβολογραμμάτων. Με τον κλασικό τρόπο μετρούνται οι θέσεις των κέντρων των κροσσών. Καθώς φαίνεται στην Εικόνα 10, οι αποκλίσεις των κροσσών από την ευθεία και τις ίσες μεταξύ τους αποστάσεις δίνουν ένα μέτρο του σφάλματος. Το σφάλμα στον προσδιορισμό της θέσεως των κέντρων των κροσσών εκφράζει το ενδογενές όριο στην ακρίβεια της κλασικής αναλύσεως και οποιεσδήποτε διακυμάνσεις στην ένταση σε σημεία του συμβολογράμματος εισάγουν επίσης σφάλματα. Καθώς τα δεδομένα των κέντρων των κροσσών είναι τα μόνα που χρησιμοποιούνται στην κλασική ανάλυση, όλη η υπόλοιπη πληροφορία που θεωρητικώς θα μπορούσε να εκμαιευθεί από τη λεπτομερή ανάλυση των διακυμάνσεων στην ένταση σε ένα συμβολόγραμμα «πετιέται στα σκουπίδια».[73][74] Τελικώς χρειάζονται περισσότερα δεδομένα στα στατικά συμβολογράμματα προκειμένου να προσδιορισθεί η πολικότητα του μετώπου του κύματος: Στην Εικόνα 10 μπορούμε να διαπιστώσουμε ότι η επιφάνεια στα δεξιά αποκλίνει από το επίπεδο, αλλά δεν μπορούμε να πούμε από αυτή μόνο την εικόνα εάν αυτή η απόκλιση είναι κοίλη ή κυρτή. Παραδοσιακά, αυτό το δεδομένο θα βρισκόταν με χρήση μη αυτόματων μέσων, όπως π.χ. παρατηρώντας την κατεύθυνση κατά την οποία μετακινούνται οι κροσσοί όταν ωθείται η επιφάνεια αναφοράς.[75]
Η PSI υπερπηδά αυτούς τους περιορισμούς επειδή δεν επαφίεται στα κέντρα των κροσσών, αλλά προχωρεί στη συλλογή δεδομένων εντάσεων στο κάθε σημείο της εικόνας που δίνει ο αισθητήρας ανιχνεύσεως. Αρκετά συμβολογράμματα (τουλάχιστον τρία) αναλύονται με την οπτική επιφάνεια αναφοράς μετατοπισμένη κατά ακριβές κλάσμα του μήκους κύματος, με χρήση ενός πιεζοηλεκτρικού μορφοτροπέα. Εναλλακτικά, ακριβείς μετατοπίσεις φάσεως μπορούν να εισαχθούν με ρύθμιση της συχνότητας του λέιζερ.[76] Οι απεικονίσεις υφίστανται επεξεργασία με υπολογιστή για τον υπολογισμό των σφαλμάτων στο οπτικό μέτωπο κύματος. Η ακρίβεια και η επαναληψιμότητα της PSI είναι πολύ μεγαλύτερες από όσο είναι δυνατό με τη στατική ανάλυση, με επαναλήψεις με ακρίβεια ενός εκατοστού του μήκους κύματος να αποτελούν πλέον ρουτίνα.[73][74] Η τεχνολογία μετατοπίσεως φάσεως έχει προσαρμοσθεί σε ποικιλία τύπων συμβολομέτρων, όπως Twyman-Green, Mach-Zehnder, λέιζερ Fizeau, ακόμα και σε κοινές διατάξεις διαδρομών, όπως στα συμβολόμετρα σημειακής περιθλάσεως.[75][77] Γενικότερα, οι τεχνικές μετατοπίσεως φάσεως μπορούν να προσαρμοσθούν σε σχεδόν οποιοδήποτε σύστημα που χρησιμοποιεί τους κροσσούς για μετρήσεις, όπως η ολογραφική συμβολομετρία και η συμβολομετρία κηλίδων.[75]
Στη συμβολομετρία σαρώσεως συμφωνίας (CSI ή VSI ή SWLI)[78] η συμβολή επιτυγχάνεται μόνο όταν οι καθυστερήσεις στο μήκος διαδρομής στο συμβολόμετρο ταιριάξουν μέσα στον χρόνο συμφωνίας της φωτεινής πηγής. Στην CSI παρακολουθείται η αντίθεση (κοντράστ) των κροσσών αντί για τη φάση τους.[2]:105 Το δείγμα (ή εναλλακτικά ο αντικειμενικός φακός) μετακινείται καθέτως και η θέση της μέγιστης αντιθέσεως φωτός-σκότους βρίσκεται για το κάθε εικονοστοιχείο του ανιχνευτή.[69][79] Το κορυφαίο πλεονέκτημα της συμβολομετρίας αυτής είναι ότι μπορούν να σχεδιασθούν συστήματα που δεν παρουσιάζουν την αμφισημία του 2 π της σύμφωνης συμβολομετρίας[80][81][82] και, όπως φαίνεται από την Εικόνα 11, που σαρώνει έναν όγκο 180μm x 140μm x 10μm, είναι κατάλληλη για την εξαγωγή του προφίλ απότομων εξάρσεων και ακανόνιστων επιφανειών. Η αξονική διακριτική ικανότητα του συστήματος καθορίζεται εν μέρει από το μήκος συμφωνίας του φωτός της πηγής.[83][84] Βιομηχανικές εφαρμογές είναι μεταξύ άλλων η μετρολογία επιφανειών, η μέτρηση των ανωμαλιών επιφανειών, η τριδιάστατη μετρολογία σε δυσκόλως προσεγγίσιμα σημεία και σε εχθρικά περιβάλλοντα, η μελέτη επιφανειών με χαρακτηριστικά μεγάλου λόγου κλίσεως (χαραγές, οπές) και η μέτρηση του πάχους μεμβρανών και επιστρώσεων (βιομηχανίες ημιαγωγών, οπτικών, κ.ά.).[85][86]
Η ολογραφική συμβολομετρία είναι μια μέθοδος που εφαρμόζει την ολογραφία για την παρακολούθηση μικρών παραμορφώσεων σε εφαρμογές με μονοχρωματική ακτινοβολία. Ακόμα όμως και σε πολλαπλά μήκη κύματος, μπορεί να χρησιμεύσει στη διαστατική μετρολογία μεγάλων αντικειμένων και στην ανίχνευση μεγαλύτερων ατελειών σε επιφάνειες.[2]:111–120 Το είδος αυτό της συμβολομετρίας ανακαλύφθηκε τυχαία ως αποτέλεσμα λαθών που είχαν σημειωθεί κατά την κατασκευή ολογραμμάτων. Τα πρώτα λέιζερ ήταν σχετικώς αδύναμα και οι φωτογραφικές πλάκες όχι τόσο ευαίσθητες, απαιτώντας έτσι μακρές χρονικώς εκθέσεις, κατά τη διάρκεια των οποίων δονήσεις ή μικρομετατοπίσεις συνέβαιναν συχνά στο οπτικό σύστημα. Τα ολογράμματα που προέκυπταν έδειχναν το αντικείμενό τους καλυμμένο με κροσσούς συμβολής και τα θεωρούσαν κατεστραμμένα.[87] Αλλά αρκετές ανεξάρτητες ομάδες πειραματιστών περί το 1965 αντιλήφθηκαν ότι οι κροσσοί εμπεριείχαν σημαντικά δεδομένα σχετικώς με μεταβολές που θα μπορούσαν να συμβαίνουν στο αντικείμενο, και άρχισαν έτσι να παράγουν σκοπίμως ολογράμματα με διπλές εκθέσεις.[88]
Η ολογραφία διπλής και πολλαπλής εκθέσεως είναι η μία μόνο από τις τρεις μεθόδους για τη δημιουργία ολογραφικών συμβολογραμμάτων. Η πρώτη έκθεση καταγράφει το αντικείμενο σε ελεύθερη κατάσταση, ενώ οι επόμενες στην ίδια φωτογραφική πλάκα το καταγράφουν υποκείμενο σε μηχανικές τάσεις. Η σύνθετη εικόνα απαθανατίζει τη διαφορά ανάμεσα στις δύο καταστάσεις.[89]
Μια δεύτερη μέθοδος είναι η ολογραφία σε πραγματικό χρόνο. Σε αυτή δημιουργείται ένα ολόγραμμα του αντικειμένου σε ελεύθερη κατάσταση και το ολόγραμμα αυτό φωτίζεται με μία δέσμη αναφοράς, οπότε παράγουμε μία δεύτερη ολογραφική απεικόνιση, υπερτεθειμένη πάνω από το αρχικό αντικείμενο που τώρα υποβάλλεται σε τάσεις. Τα κύματα του ειδώλου του αντικειμένου από αυτό το ολόγραμμα θα συμβάλουν με τα νέα κύματα που έρχονται από το αντικείμενο. Η τεχνική αυτή επιτρέπει την παρακολούθηση μικρομεταβολών του σχήματος του αντικειμένου σε πραγματικό χρόνο.[89]
Η τρίτη μέθοδος, η ολογραφία μέσου χρονικού όρου (time-average holography), συνίσταται στη δημιουργία ενός ολογράμματος ενώ το αντικείμενο υποβάλλεται σε περιοδικές μηχανικές τάσεις ή δονήσεις. Αυτή η μέθοδος δίνει μια οπτική απεικόνιση του «μοτίβου» των δονήσεων.[89]
-
Εικόνα 12. Απεικόνιση με InSAR του ηφαιστείου Κιλαουέα της Χαβάης, με κροσσούς συμβολής που προκλήθηκαν από παραμορφώσεις του εδάφους στη διάρκεια ενός εξαμήνου.
-
Εικόνα 13. Κροσσοί ESPI που δείχνουν έναν τρόπο ταλαντώσεως μιας στερεωμένης τετράγωνης πλάκας.
Το συμβολομετρικό ραντάρ συνθετικού διαμετρήματος (InSAR) είναι μια τεχνική ραντάρ που βρίσκει εφαρμογή στη γεωδαισία και στην τηλεπισκόπηση. Δορυφορικές απεικονίσεις με ραντάρ συνθετικού διαμετρήματος (SAR) ενός γεωγραφικού χαρακτηριστικού λαμβάνονται σε διαφορετικές ημέρες και όσες μεταβολές έχουν συμβεί στο ενδιάμεσο χρονικό διάστημα καταγράφονται ως κροσσοί, παρόμοιοι με αυτούς της ολογραφικής συμβολομετρίας. Η τεχνική αυτή μπορεί να καταγράφει παραμορφώσεις της τάξεως των εκατοστών ή και χιλιοστών του μέτρου, που οφείλονται σε ηφαιστειακή ή σεισμική δραστηριότητα, ή σε κατολισθήσεις. Βρίσκει επίσης εφαρμογή στη δομική μηχανική, ιδίως στην παρακολούθηση της δομικής σταθερότητας. Η Εικόνα 12 δείχνει το ενεργό ηφαίστειο Κιλαουέα της Χαβάης. Δεδομένα που συλλέχθηκαν με χρήση του SAR του Διαστημικού Λεωφορείου Εντέβορ στις 13 Απριλίου 13 1994 και στις 4 Οκτωβρίου 1994 χρησιμοποιήθηκαν για τη δημιουργία συμβολομετρικών κροσσών, που υπερτέθηκαν στην εικόνα SAR του Κιλαουέα.[90]
Η ηλεκτρονική συμβολομετρία κατανομής κηλίδων (ESPI), γνωστή και ως «ολογραφία TV», χρησιμοποιεί ανίχνευση με βιντεοκάμερες και καταγραφή για να δημουργήσει μια εικόνα του αντικειμένου επί της οποίας υπερτίθεται ένα σύνολο κροσσών που αντιπροσωπεύει τη μετατόπιση του αντικειμένου μεταξύ δύο καταγραφών (δείτε Εικόνα 13). Οι κροσσοί είναι παρόμοιοι με εκείνους που προκύπτουν από την ολογραφική συμβολομετρία.[2]:111–120[91]
Αρχικώς μετά την εφεύρεση των λέιζερ, η κηλίδωση εξαιτίας των σύμφωνων κυμάτων (λόγω τυχαίας συμβολής) θεωρήθηκε σοβαρό εμπόδιο στη χρήση λέιζερ για τον φωτισμό αντικειμένων, ιδίως στην ολογραφική απεικόνιση εξαιτίας της κοκκώδους εικόνας που προέκυπτε. Αργότερα έγινε αντιληπτό ότι η κατανομή των κηλίδων μπορούσε να πληροφορίες σχετικώς με τις παραμορφώσεις της επιφάνειας του αντικειμένου. Οι Butters και Leendertz ανέπτυξαν την τεχνική της συμβολομετρίας κηλίδων (speckle pattern interferometry)[92] το 1970 και από τότε έχει εφαρμοσθεί σε διάφορες άλλες δραστηριότητες. Μια φωτογραφία των κηλίδων λαμβάνεται πριν την παραμόρφωση, μία δεύτερη φωτογραφία λαμβάνεται μετά την παραμόρφωση. Η ψηφιακή αφαίρεση των δύο εικόνων δίνει μία συσχέτιση, στην οποία οι κροσσοί αντιπροσωπεύουν γραμμές ίσης παραμορφώσεως. Παλμοί λέιζερ με διάρκεια της τάξεως των νανοδευτερολέπτων μπορούν να χρησιμοποιηθούν για να συλλάβουν πολύ μικρής διάρκειας προσωρινά γεγονότα. Υπάρχει ένα πρόβλημα με τη φάση: Με την απουσία άλλων πληροφοριών είναι αδύνατη η διάκριση ανάμεσα σε περιγράμματα (γραμμές) που αντιστοιχούν σε μια κορυφή κύματος και σε περιγράμματα που αντιστοιχούν σε βύθισμα. Προκειμένου να διευκρινισθεί το θέμα, η ESPI μπορεί να συνδυασθεί με μεθόδους μεταθέσεως φάσεως.[93][94]
Μια μέθοδος καθορισμού γεωδαιτικών γραμμών βάσεων με ακρίβεια, που επινοήθηκε από τον Ούργιο Βάισαλα, εκμεταλλεύθηκε το μικρό μήκος συμφωνίας που έχει το λευκό φως: Αρχικώς το λευκό φως χωρίζεται σε δύο δέσμες, με τη δέσμη αναφοράς «διπλωμένη», να πηγαινοέρχεται 6 φορές ανάμεσα σε ένα ζεύγος κατόπτρων τοποθετημένων σε απόσταση ακριβώς 1 μέτρου το ένα από το άλλο. Μόνο όταν η διαδρομή της άλλης δέσμης ήταν ακριβώς εξαπλάσια της διαδρομής αναφοράς μπορούσαν να παρατηρηθούν κροσσοί. Επαναλαμβανόμενες εφαρμογές της μεθόδου αυτής επέτρεψαν την ακριβή μέτρηση αποστάσεων έως και 864 μέτρων. Οι γραμμές βάσεως που καθορίζονται έτσι χρησίμευσαν για τη βαθμονόμηση εξοπλισμού γεωδαιτικών μετρήσεων αποστάσεων, και τελικώς για τη δημιουργία μιας μετρολογικώς αναγώγιμης κλίμακας για τα γεωδαιτικά δίκτυα που μετρούνται από τα όργανα αυτά.[95] (Η μέθοδος αυτή έχει δώσει τη θέση της σημέρα στις μετρήσεις με GPS.)
Συμβολόμετρα έχουν χρησιμοποιηθεί εκτός των παραπάνω για τη μελέτη της διαχύσεως υλικών, για τη μέτρηση σύνθετων δεικτών διαθλάσεως και θερμικών ιδιοτήτων. Επίσης, για την απεικόνιση-χαρτογράφηση τριδιάστατης κινήσεως, όπως των τρόπων ταλαντώσεων διάφορων δομών.[71]
Βιολογία και ιατρική
ΕπεξεργασίαΕφαρμοζόμενη στη βιολογία και την ιατρική, η οπτική συμβολομετρία παρέχει και πάλι δυνατότητες για πολύ ακριβείς και ευαίσθητες μετρήσεις βιομορίων, οργανιδίων του κυττάρου, κυττάρων και ιστών.[96] Πολλές μορφές βιοαισθητήρων βασίζονται στη συμβολομετρία, επειδή η απευθείας αλληλεπίδραση των ηλεκτρομαγνητικών πεδίων με την τοπική μοριακή πολωσιμότητα αναιρεί την ανάγκη για φθορίζουσες σημάνσεις ή σήμανση με νανοσωματίδια. Σε μια μεγαλύτερη κλίμακα, η κυτταρική συμβολομετρία μοιράζεται κάποια κοινά με τη μικροσκοπία αντιθέσεως φάσεων, αλλά συνιστά μια πολύ μεγαλύτερη τάξη ευαίσθητων στη φάση οπτικών διατάξεων, που βασίζονται στη συμβολή ανάμεσα σε μέρη των κυττάρων μέσα από τη διάθλαση και την περίθλαση. Στην κλίμακα των ιστών, η διάδοση μερικώς σύμφωνου, εμπροσθοσκεδαζόμενου φωτός μέσα από μικροαποκλίσεις και την ετερογένεια των δομών του ιστού παρέχει δυνατότητες για τη χρήση τομογραφίας οπτικής συμφωνίας και φασματοσκοπίας των διακυμάνσεων (ευαίσθητης στη φάση) για την απεικόνιση λεπτών δομικών και δυναμικών ιδιοτήτων.
| Εικόνα 14. Τυπική οπτική διάταξη σημειακής OCT. |
Εικόνα 15. Κεντρική ορρώδης αμφιβληστροειδοπάθεια απεικονισμένη με τομογραφία. |
Η τομογραφία οπτικής συμφωνίας (OCT) είναι μια τεχνική ιατρικής απεικονίσεως που εφαρμόζει συμβολομετρία μικρής συμφωνίας για να αποκτήσει τομογραφικές εικόνες εσωτερικών μικροδομών των ιστών. Στην Εικόνα 14 το κέντρο ενός τυπικού συστήματος OCT είναι ένα συμβολόμετρο Μάικελσον. Ο ένας βραχίονας του συμβολομέτρου είναι εστιασμένος πάνω στον υπό εξέταση ιστό και τον σαρώνει με καρτεσιανό τρόπο X-Y. Ο άλλος βραχίονας του συμβολομέτρου ανακλάται από ένα κάτοπτρο αναφοράς. Το φως τώρα που ανακλάται από τον ιστό συμβάλλει με το φως που ανακλάται από το κάτοπτρο αναφοράς. Εξαιτίας της μικρής συμφωνίας της πηγής του φωτός, το συμβολομετρικό σήμα παρατηρείται μόνο για ένα περιορισμένο πάχος (βάθος) ιστού. Η σάρωση X-Y καταγράφει έτσι μία λεπτή φέτα του δείγματος κάθε φορά. Με την εκτέλεση πολλαπλών σαρώσεων, κινώντας το κάτοπτρο αναφοράς μετά την κάθε σάρωση, μπορεί να κατασκευασθεί μία ολόκληρη τριδιάστατη απεικόνιση του ιστού.[97][98] Πρόσφατες εξελίξεις επεχείρησαν να συνδυάσουν την ανάκτηση φάσεως της σύμφωνης συμβολομετρίας με την ικανότητα για τη μέτρηση αποστάσεων της συμβολομετρίας μικρής συμφωνίας.[71]
-
Εικόνα 16. Κύτταρο από νήμα φύκους υπό αντίθεση φάσεως.
-
Εικόνα 17. Ωοκύστη του Toxoplasma gondii απεικονισμένη με μικροσκοπία DIC
-
Εικόνα 18. Υψηλής αναλύσεως απεικόνιση μιας αράχνης με αντίθεση φάσεως στις ακτίνες Χ.
Η μικροσκοπία αντιθέσεως φάσεως (phase-contrast microscopy) και η μικροσκοπία διαφορικής αντιθέσεως συμβολής (differential interference contrast, DIC) είναι σημαντικά εργαλεία στη βιολογία και την ιατρική. Τα περισσότερα κύτταρα ζώων και μονοκύτταρων οργανισμών έχουν ελάχιστο δικό τους χρώμα και τα ενδοκυτταρικά οργανίδια είναι σχεδόν τελείως αόρατα με τον συνηθισμένο φωτισμό εκ των κάτω. Αυτές οι δομές μπορούν να καταστούν ορατές με χρώση των δειγμάτων, αλλά οι διαδικασίες της χρώσεως είναι χρονοβόρες και σκοτώνουν τα κύτταρα. Καθώς φαίνεται στις Εικόνες 16 και 17, τα μικροσκόπια αντιθέσεως φάσεως και DIC επιτρέπουν την εξέταση μη χρωσμένων, ζωντανών κυττάρων.[99] Η DIC έχει και μη βιολογικές εφαρμογές, όπως στην ανάλυση επίπεδης επεξεργασίας ημιαγωγών πυριτίου.
Η συμβολομετρία διακρίσεως γωνίας και μικρής συμφωνίας (angle-resolved low-coherence interferometry, a/LCI) μετρεί με σκεδαζόμενο φως τα μεγέθη υποκυτταρικών σωμάτων, όπως είναι οι πυρήνες των κυττάρων. Αυτό επιτρέπει να συνδυασθούν συμβολομετρικές μετρήσεις βάθους με μετρήσεις πυκνότητας. Διάφοροι συσχετισμοί έχουν βρεθεί ανάμεσα στο πόσο υγιής είναι ο ιστός και στις μετρήσεις σε υποκυτταρικές δομές. Π.χ. έχει ότι καθώς ο ιστός μεταβάλλεται από κανονικό σε καρκινικό, το μέσο μέγεθος των κυτταρικών πυρήνων αυξάνεται.[100][101]
Η απεικόνιση αντιθέσεως φάσεως στις ακτίνες Χ (Εικόνα 26) είναι ένας όρος που περιλαμβάνει ποικιλία τεχνικών που αρύονται δεδομένα που προκύπτουν από τη φάση μιας σύμφωνης δέσμης ακτίνων Χ προκειμένου να απεικονίσουν μαλακούς ιστούς. Αυτή έχει καταστεί μια σημαντική μέθοδος για την απεικόνιση κυτταρικών και ιστολογικών δομών σε μια ευρεία ποικιλία βιολογικών και ιατρικών μελετών. Υπάρχουν αρκετές τεχνολογίες σε χρήση για την απεικόνιση αντιθέσεως φάσεως στις ακτίνες Χ, που χρησιμοποιούν διαφορετικές αρχές προκειμένου να μετατρέψουν τις διακυμάνσεις φάσεως στις ακτίνες Χ που έρχονται από ένα σώμα σε διακυμάνσεις εντάσεως.[102][103] Αυτές οι τεχνολογίες περιλαμβάνουν την αντίθεση φάσεως με βάση τη διάδοση των ακτίνων[104], τη συμβολομετρία φαινομένου Τάλμποτ[103], τη βασισμένη στα σχέδια Μουαρέ συμβολομετρία μακρού[105], ενισχυμένη δια της διαθλάσεως απεικόνιση[106] και η συμβολομετρία ακτίνων Χ[107]. Αυτές οι μέθοδοι παρέχουν υψηλότερη αντίθεση («κοντράστ») σε σύγκριση με την απλή απεικόνιση στις ακτίνες Χ (αντίθεση από απορρόφηση), καθιστώντας δυνατή την παρατήρηση μικρότερων λεπτομερειών. Ένα μειονέκτημα είναι ότι οι παραπάνω μέθοδοι απαιτούν πιο πολύπλοκο εξοπλισμό, όπως ένα μικρό σύγχροτρο ή σωλήνα ακτίνων Χ μικροεστιάσεως ως πηγές, και οπτική ακτίνων Χ ή ανιχνευτές ακτίνων Χ υψηλής αναλύσεως.
Δείτε επίσης
Επεξεργασία- Ολογραφία
- Αρχή της επαλληλίας (ή της υπερθέσεως)
Παραπομπές
Επεξεργασία- ↑ Bunch, Bryan H.· Hellemans, Alexander (Απρίλιος 2004). The History of Science and Technology . Houghton Mifflin Harcourt. σελ. 695. ISBN 978-0-618-22123-3.
- ↑ 2,00 2,01 2,02 2,03 2,04 2,05 2,06 2,07 2,08 2,09 2,10 2,11 2,12 2,13 2,14 Hariharan, P. (2007). Basics of Interferometry. Elsevier Inc. ISBN 978-0-12-373589-8.
- ↑ Patel, R.; Achamfuo-Yeboah, S.; Light R.; Clark M. (2014). «Widefield two laser interferometry». Optics Express 22 (22): 27094-27101. doi:. PMID 25401860. Bibcode: 2014OExpr..2227094P. https://www.osapublishing.org/oe/abstract.cfm?uri=oe-22-22-27094.
- ↑ T.Young: «The Bakerian Lecture:Experiments and Calculations Relative to Physical Optics», Philosophical Transactions of the Royal Society of London, τόμ. 94 (έτος 1804), σσ. 1-16
- ↑ Kipnis, Nahum (1991). History of the Principle of Interference of Light. doi:10.1007/978-3-0348-8652-9. ISBN 978-3-0348-9717-4.
- ↑ J. Lequeux: François Arago, A 19th Century French Humanist and Pioneer in Astrophysics, Springer International Publishing - Imprint: Springer, 2015
- ↑ Nolte, David D. (2023). Interference: The History of Optical Interferometry and the Scientists Who Tamed Light (Oxford University Press, 2023). Oxford University Press. ISBN 978-0192869760.
- ↑ Nolte: Interference, σελ. 111
- ↑ 9,0 9,1 9,2 9,3 Paschotta, Rüdiger. «Optical Heterodyne Detection». RP Photonics Consulting GmbH. Ανακτήθηκε στις 1 Απριλίου 2012.
- ↑ Poole, Ian. «The superhet or superheterodyne radio receiver». Radio-Electronics.com. Ανακτήθηκε στις 22 Ιουνίου 2012.
- ↑ Mallick, S.· Malacara, D. (2007). «Common-Path Interferometers». Optical Shop Testing. σελ. 97. doi:10.1002/9780470135976.ch3. ISBN 978-0-470-13597-6.
- ↑ Verma, R.K. (2008). Wave Optics. Discovery Publishing House. σελίδες 97–110. ISBN 978-81-8356-114-3.
- ↑ Kolesnichenko, Pavel; Wittenbecher, Lukas; Zigmantas, Donatas (2020). «Fully symmetric dispersionless stable transmission-grating Michelson interferometer». Optics Express 28 (25): 37752-37757. doi:. PMID 33379604. Bibcode: 2020OExpr..2837752K.
- ↑ «Interferential Devices – Introduction». OPI – Optique pour l'Ingénieur. Ανακτήθηκε στις 1 Απριλίου 2012.
- ↑ Ingram Taylor, Sir Geoffrey (1909). «Interference Fringes with Feeble Light». Proc. Camb. Phil. Soc. 15: 114. http://www.physics.wisc.edu/undergrads/courses/spring09/205/handouts/GITaylor_Interference.pdf. Ανακτήθηκε στις 2 January 2013.
- ↑ Jönsson, C. (1961). «Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten». Zeitschrift für Physik 161 (4): 454-474. doi:. Bibcode: 1961ZPhy..161..454J.
- ↑ Jönsson, C. (1974). «Electron diffraction at multiple slits». American Journal of Physics 4 (1): 4-11. doi:. Bibcode: 1974AmJPh..42....4J.
- ↑ Arndt, M.· Zeilinger, A. (2004). «Heisenberg's Uncertainty and Matter Wave Interferometry with Large Molecules». Στο: Buschhorn, G.W.· Wess, J., επιμ. Fundamental Physics – Heisenberg and Beyond: Werner Heisenberg Centennial Symposium "Developments in Modern Physics". Springer. σελίδες 35–52. ISBN 978-3-540-20201-1.
- ↑ Carroll, Brett. «Simple Lloyd's Mirror» (PDF). American Association of Physics Teachers. Ανακτήθηκε στις 5 Απριλίου 2012.
- ↑ Serway, R.A.· Jewett, J.W. (2010). Principles of physics: a calculus-based text, Volume 1. Brooks Cole. σελ. 905. ISBN 978-0-534-49143-7.
- ↑ «Guideline for Use of Fizeau Interferometer in Optical Testing» (PDF). NASA. Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 25 Σεπτεμβρίου 2018. Ανακτήθηκε στις 8 Απριλίου 2012.
- ↑ «Interferential devices – Fizeau Interferometer». Optique pour l'Ingénieur. Ανακτήθηκε στις 8 Απριλίου 2012.
- ↑ Zetie, K.P.· Adams, S.F.· Tocknell, R.M. «How does a Mach–Zehnder interferometer work?» (PDF). Physics Department, Westminster School, London. Ανακτήθηκε στις 8 Απριλίου 2012.
- ↑ Ashkenas, Harry I. (1950). The design and construction of a Mach–Zehnder interferometer for use with the GALCIT Transonic Wind Tunnel. Engineer's thesis (engd). California Institute of Technology. doi:10.7907/D0V1-MJ80.
- ↑ Betzler, Klaus. «Fabry–Perot Interferometer» (PDF). Fachbereich Physik, Universität Osnabrück. Ανακτήθηκε στις 8 Απριλίου 2012.
- ↑ Nolte, David D. (2012). Optical Interferometry for Biology and Medicine. Springer. σελίδες 17–26. Bibcode:2012oibm.book.....N. ISBN 978-1-4614-0889-5.
- ↑ Michelson, A.A.; Morley, E.W. (1887). «On the Relative Motion of the Earth and the Luminiferous Ether». American Journal of Science 34 (203): 333-345. doi:. Bibcode: 1887AmJS...34..333M. http://www.aip.org/history/exhibits/gap/PDF/michelson.pdf. Ανακτήθηκε στις 2012-04-09.
- ↑ Miller, Dayton C. (1933). «The Ether-Drift Experiment and the Determination of the Absolute Motion of the Earth». Reviews of Modern Physics 5 (3): 203-242. doi:. Bibcode: 1933RvMP....5..203M. «White light fringes were chosen for the observations because they consist of a small group of fringes having a central, sharply defined black fringe which forms a permanent zero reference mark for all readings.».
- ↑ Müller, H.; Herrmann, S.; Braxmaier, C.; Schiller, S.; Peters, A. (2003). «Modern Michelson–Morley experiment using cryogenic optical resonators». Phys. Rev. Lett. 91 (2): 020401. doi:. PMID 12906465. Bibcode: 2003PhRvL..91b0401M.
- ↑ Eisele, C.; Nevsky, A.; Schiller, S. (2009). «Laboratory Test of the Isotropy of Light Propagation at the 10-17 Level». Physical Review Letters 103 (9): 090401. doi:. PMID 19792767. Bibcode: 2009PhRvL.103i0401E.
- ↑ Herrmann, S.; Senger, A.; Möhle, K.; Nagel, M.; Kovalchuk, E.; Peters, A. (2009). «Rotating optical cavity experiment testing Lorentz invariance at the 10-17 level». Physical Review D 80 (10): 105011. doi:. Bibcode: 2009PhRvD..80j5011H.
- ↑ Scherrer, P.H.; Bogart, R.S.; Bush, R.I.; Hoeksema, J.; Kosovichev, A.G.; Schou, J. (1995). «The Solar Oscillations Investigation – Michelson Doppler Imager». Solar Physics 162 (1-2): 129-188. doi:. Bibcode: 1995SoPh..162..129S.
- ↑ Stroke, G.W.; Funkhouser, A.T. (1965). «Fourier-transform spectroscopy using holographic imaging without computing and with stationary interferometers». Physics Letters 16 (3): 272-274. doi:. Bibcode: 1965PhL....16..272S. http://deepblue.lib.umich.edu/bitstream/2027.42/32013/1/0000055.pdf. Ανακτήθηκε στις 2 April 2012.
- ↑ Gary, G.A.· Balasubramaniam, K.S. «Additional Notes Concerning the Selection of a Multiple-Etalon System for ATST» (PDF). Advanced Technology Solar Telescope. Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 10 Αυγούστου 2010. Ανακτήθηκε στις 29 Απριλίου 2012.
- ↑ «Spectrometry by Fourier transform». OPI – Optique pour l'Ingénieur. Ανακτήθηκε στις 3 Απριλίου 2012.
- ↑ «LIGO-Laser Interferometer Gravitational-Wave Observatory». Caltech/MIT. Ανακτήθηκε στις 4 Απριλίου 2012.
- ↑ Castelvecchi, Davide; Witze, Alexandra (11 February 2016). «Einstein's gravitational waves found at last». Nature News. doi:. http://www.nature.com/news/einstein-s-gravitational-waves-found-at-last-1.19361. Ανακτήθηκε στις 11 February 2016.
- ↑ Chevalerias, R.; Latron, Y.; Veret, C. (1957). «Methods of Interferometry Applied to the Visualization of Flows in Wind Tunnels». Journal of the Optical Society of America 47 (8): 703. doi:. Bibcode: 1957JOSA...47..703C.
- ↑ Ristić, Slavica. «Flow visualization techniques in wind tunnels – optical methods (Part II)» (PDF). Military Technical Institute, Serbia. Ανακτήθηκε στις 6 Απριλίου 2012.
- ↑ Paris, M.G.A. (1999). «Entanglement and visibility at the output of a Mach-Zehnder interferometer». Physical Review A 59 (2): 1615-1621. doi:. Bibcode: 1999PhRvA..59.1615P. Αρχειοθετήθηκε από το πρωτότυπο στις 2016-09-10. https://web.archive.org/web/20160910074215/http://qinf.fisica.unimi.it/~paris/PDF/visent.pdf. Ανακτήθηκε στις 2 April 2012.
- ↑ Haack, G.R.; Förster, H.; Büttiker, M. (2010). «Parity detection and entanglement with a Mach-Zehnder interferometer». Physical Review B 82 (15): 155303. doi:. Bibcode: 2010PhRvB..82o5303H.
- ↑ 42,0 42,1 Monnier, John D. (2003). «Optical interferometry in astronomy». Reports on Progress in Physics 66 (5): 789-857. doi:. Bibcode: 2003RPPh...66..789M. http://www.astro.lsa.umich.edu/~monnier/Publications/ROP2003_final.pdf.
- ↑ «Cosmic Calibration». www.eso.org. Ανακτήθηκε στις 10 Οκτωβρίου 2016.
- ↑ Malbet, F.; Kern, P.; Schanen-Duport, I.; Berger, J.-P.; Rousselet-Perraut, K.; Benech, P. (1999). «Integrated optics for astronomical interferometry». Astron. Astrophys. Suppl. Ser. 138: 135-145. doi:. Bibcode: 1999A&AS..138..135M.
- ↑ Baldwin, J.E.; Haniff, C.A. (2002). «The application of interferometry to optical astronomical imaging». Phil. Trans. R. Soc. Lond. A 360 (1794): 969-986. doi:. PMID 12804289. Bibcode: 2002RSPTA.360..969B.
- ↑ Gerlich, S.; Eibenberger, S.; Tomandl, M.; Nimmrichter, S.; Hornberger, K.; Fagan, P.J.; Tüxen, J.; Mayor, M. και άλλοι. (2011). «Quantum interference of large organic molecules». Nature Communications 2: 263. doi:. PMID 21468015. Bibcode: 2011NatCo...2..263G.
- ↑ Hornberger, Klaus; Gerlich, Stefan; Haslinger, Philipp; Nimmrichter, Stefan; Arndt, Markus (2012-02-08). «Quantum interference of clusters and molecules». Reviews of Modern Physics 84 (1): 157-173. doi:. Bibcode: 2012RvMP...84..157H.
- ↑ Eibenberger, Sandra; Gerlich, Stefan; Arndt, Markus; Mayor, Marcel; Tüxen, Jens (2013-08-14). «Matter–wave interference of particles selected from a molecular library with masses exceeding 10000 amu». Physical Chemistry Chemical Physics 15 (35): 14696-14700. doi:. ISSN 1463-9084. PMID 23900710. Bibcode: 2013PCCP...1514696E.
- ↑ Lehmann, M.; Lichte, H. (Δεκέμβριος 2002). «Tutorial on off-axis electron holography». Microsc. Microanal. 8 (6): 447-466. doi:. PMID 12533207. Bibcode: 2002MiMic...8..447L.
- ↑ Tonomura, A. (1999). Electron Holography (2η έκδοση). Springer. ISBN 978-3-540-64555-9.
- ↑ Klein, T. (2009). «Neutron interferometry: A tale of three continents». Europhysics News 40 (6): 24-26. doi:. Bibcode: 2009ENews..40f..24K.
- ↑ Dimopoulos, S.; Graham, P.W.; Hogan, J.M.; Kasevich, M.A. (2008). «General Relativistic Effects in Atom Interferometry». Phys. Rev. D 78 (42003): 042003. doi:. Bibcode: 2008PhRvD..78d2003D.
- ↑ Mariani, Z.; Strong, K.; Wolff, M. (2012). «Infrared measurements in the Arctic using two Atmospheric Emitted Radiance Interferometers». Atmos. Meas. Tech. 5 (2): 329-344. doi:. Bibcode: 2012AMT.....5..329M.
- ↑ Mantravadi, M.V.· Malacara, D. (2007). «Newton, Fizeau, and Haidinger Interferometers». Optical Shop Testing. σελ. 1. doi:10.1002/9780470135976.ch1. ISBN 978-0-470-13597-6.
- ↑ Malacara, D. (2007). «Twyman–Green Interferometer». Optical Shop Testing. σελίδες 46–96. doi:10.1002/9780470135976.ch2. ISBN 978-0-470-13597-6.
- ↑ Michelson, A.A. (1918). «On the Correction of Optical Surfaces». Proceedings of the National Academy of Sciences of the United States of America 4 (7): 210-212. doi:. PMID 16576300. Bibcode: 1918PNAS....4..210M.
- ↑ Heideman, R.G.; Kooyman, R.P.H.; Greve, J. (1993). «Performance of a highly sensitive optical waveguide Mach–Zehnder interferometer immunosensor». Sensors and Actuators B: Chemical 10 (3): 209-217. doi:. Bibcode: 1993SeAcB..10..209H.
- ↑ Oliver, W.D.; Yu, Y.; Lee, J.C.; Berggren, K.K.; Levitov, L.S.; Orlando, T.P. (2005). «Mach–Zehnder Interferometry in a Strongly Driven Superconducting Qubit». Science 310 (5754): 1653-1657. doi:. PMID 16282527. Bibcode: 2005Sci...310.1653O.
- ↑ Nieradko, Ł.; Gorecki, C.; JóZwik, M.; Sabac, A.; Hoffmann, R.; Bertz, A. (2006). «Fabrication and optical packaging of an integrated Mach–Zehnder interferometer on top of a movable micromirror». Journal of Micro/Nanolithography, MEMS, and MOEMS 5 (2): 023009. doi:. Bibcode: 2006JMM&M...5b3009N.
- ↑ Burge, J.H.· Zhao, C.· Dubin, M. (2010). «Measurement of aspheric mirror segments using Fizeau interferometry with CGH correction» (PDF). Modern Technologies in Space- and Ground-based Telescopes and Instrumentation. Proceedings of SPIE. 7739. σελ. 773902. Bibcode:2010SPIE.7739E..02B. doi:10.1117/12.857816.
- ↑ Anderson, R.; Bilger, H.R.; Stedman, G.E. (1994). «"Sagnac effect" A century of Earth-rotated interferometers». Am. J. Phys. 62 (11): 975-985. doi:. Bibcode: 1994AmJPh..62..975A. Αρχειοθετήθηκε από το πρωτότυπο στις 2019-11-30. https://web.archive.org/web/20191130214457/http://signallake.com/innovation/andersonNov94.pdf. Ανακτήθηκε στις 30 March 2012.
- ↑ Golio, Mike (2007). RF and Microwave Applications and Systems. CRC Press. σελίδες 14.1–14.17. ISBN 978-0-8493-7219-3. Ανακτήθηκε στις 27 Ιουνίου 2012.
- ↑ Paschotta, Rüdiger. «Self-heterodyne Linewidth Measurement». RP Photonics. Ανακτήθηκε στις 22 Ιουνίου 2012.
- ↑ «Optical Frequency Comb». National Research Council, Canada. Αρχειοθετήθηκε από το πρωτότυπο στις 5 Μαρτίου 2012. Ανακτήθηκε στις 23 Ιουνίου 2012.
- ↑ Paschotta, Rüdiger. «Frequency Combs». RP Photonics. Ανακτήθηκε στις 23 Ιουνίου 2012.
- ↑ Schmit, J. (1993). «Spatial and temporal phase-measurement techniques: a comparison of major error sources in one dimension». Στο: Brown, Gordon M.· Kwon, Osuk Y.· Kujawinska, Malgorzata· Reid, Graeme T., επιμ. Proceedings of SPIE. Interferometry: Techniques and Analysis. 1755. σελίδες 202–201. doi:10.1117/12.140770.
- ↑ Larkin, K.G. (1996). «Efficient nonlinear algorithm for envelope detection in white light interferometry». Journal of the Optical Society of America 13 (4): 832–843. doi:. Bibcode: 1996JOSAA..13..832L. Αρχειοθετήθηκε από το πρωτότυπο στις 2020-03-10. https://web.archive.org/web/20200310165204/https://nontrivialzeros.net/KGL_Papers/23_Neat_Algorithm_JOSAA96.pdf. Ανακτήθηκε στις 1 April 2012.
- ↑ ISO. (2013). 25178-604:2013(E): Geometrical product specification (GPS) – Surface texture: Areal – Nominal characteristics of non-contact (coherence scanning interferometric microscopy) instruments, International Organization for Standardization Γενεύη 2013
- ↑ 69,0 69,1 Harasaki, A.; Schmit, J.; Wyant, J.C. (2000). «Improved vertical-scanning interferometry». Applied Optics 39 (13): 2107-2115. doi:. PMID 18345114. Bibcode: 2000ApOpt..39.2107H. Αρχειοθετήθηκε από το πρωτότυπο στις 2010-07-25. https://web.archive.org/web/20100725084235/http://www.optics.arizona.edu/jcwyant/pdf/Published_Papers/Optical_Profiler/Improved%20Vertical-Scanning%20Interferometry.pdf. Ανακτήθηκε στις 21 May 2012.
- ↑ De Groot, P. (2015). «Principles of interference microscopy for the measurement of surface topography». Advances in Optics and Photonics 7 (1): 1-65. doi:. Bibcode: 2015AdOP....7....1D.
- ↑ 71,0 71,1 71,2 Olszak, A.G.· Schmit, J.· Heaton, M.G. «Interferometry: Technology and Applications» (PDF). Bruker. Ανακτήθηκε στις 1 Απριλίου 2012.
- ↑ de Groot, Peter; Deck, Leslie (1995). «Surface Profiling by Analysis of White-light Interferograms in the Spatial Frequency Domain». Journal of Modern Optics 42 (2): 389-401. doi:. Bibcode: 1995JMOp...42..389D.
- ↑ 73,0 73,1 «Phase-Shifting Interferometry for Determining Optical Surface Quality». Newport Corporation. Αρχειοθετήθηκε από το πρωτότυπο στις 7 Νοεμβρίου 2012. Ανακτήθηκε στις 12 Μαΐου 2012.
- ↑ 74,0 74,1 «How Phase Interferometers work». Graham Optical Systems. 2011. Ανακτήθηκε στις 12 Μαΐου 2012.
- ↑ 75,0 75,1 75,2 Schreiber, H.· Bruning, J.H. (2007). «Phase Shifting Interferometry». Optical Shop Testing. σελ. 547. doi:10.1002/9780470135976.ch14. ISBN 978-0-470-13597-6.
- ↑ Sommargren, G.E. (1986), US Patent 4,594,003
- ↑ Ferraro, P.· Paturzo, M.· Grilli, S. (2007). «Optical wavefront measurement using a novel phase-shifting point-diffraction interferometer». SPIE. Ανακτήθηκε στις 26 Μαΐου 2012.
- ↑ P. de Groot, J.: «Interference Microscopy for Surface Structure Analysis», στο Handbook of Optical Metrology, επιμ. T. Yoshizawa, κεφ. 31, σσ. 791-828, CRC Press, 2015
- ↑ «HDVSI – Introducing High Definition Vertical Scanning Interferometry for Nanotechnology Research from Veeco Instruments». Veeco. Αρχειοθετήθηκε από το πρωτότυπο στις 9 Απριλίου 2012. Ανακτήθηκε στις 21 Μαΐου 2012.
- ↑ Plucinski, J.; Hypszer, R.; Wierzba, P.; Strakowski, M.; Jedrzejewska-Szczerska, M.; Maciejewski, M.; Kosmowski, B.B. (2008). «Optical low-coherence interferometry for selected technical applications». Bulletin of the Polish Academy of Sciences 56 (2): 155-172. http://bulletin.pan.pl/(56-2)155.pdf. Ανακτήθηκε στις 8 April 2012.
- ↑ Yang, C.-H.; Wax, A.; Dasari, R.R.; Feld, M.S. (2002). «2π ambiguity-free optical distance measurement with subnanometer precision with a novel phase-crossing low-coherence interferometer». Optics Letters 27 (2): 77-79. doi:. PMID 18007717. Bibcode: 2002OptL...27...77Y. http://authors.library.caltech.edu/3326/1/YANol02b.pdf.
- ↑ Hitzenberger, C.K.; Sticker, M.; Leitgeb, R.; Fercher, A.F. (2001). «Differential phase measurements in low-coherence interferometry without 2pi ambiguity». Optics Letters 26 (23): 1864-1866. doi:. PMID 18059719. Bibcode: 2001OptL...26.1864H.
- ↑ Wojtek J. Walecki, Kevin Lai, Vitalij Souchkov, Phuc Van, S.H. Lau, Ann Koo: Physica Status Solidi C, τόμ. 2, τεύχ. 3, σσ. 984-989
- ↑ W.J. Walecki κ.ά.: «Non-contact fast wafer metrology for ultra-thin patterned wafers mounted on grinding and dicing tapes», Electronics Manufacturing Technology Symposium, 2004, IEEE/CPMT/SEMI, 29th International Volume, Issue, 14-16 Ιουλίου 2004, σσ. 323-325
- ↑ «Coating Thickness Measurement». Lumetrics, Inc. Αρχειοθετήθηκε από το πρωτότυπο στις 29 Οκτωβρίου 2013. Ανακτήθηκε στις 28 Οκτωβρίου 2013.
- ↑ «Typical profilometry measurements». Novacam Technologies, Inc. Ανακτήθηκε στις 25 Ιουνίου 2012.
- ↑ «Holographic interferometry». Oquagen. 2008. Ανακτήθηκε στις 22 Μαΐου 2012.
- ↑ Hecht, Jeff (1998). Laser, Light of a Million Uses. Dover Publications, Inc. σελίδες 229–230. ISBN 978-0-486-40193-5.
- ↑ 89,0 89,1 89,2 Fein, H. (Σεπτέμβριος 1997). «Holographic Interferometry: Nondestructive tool». The Industrial Physicist: 37-39. http://www.aip.org/tip/INPHFA/vol-3/iss-3/p37.pdf.
- ↑ «PIA01762: Space Radar Image of Kilauea, Hawaii». NASA/JPL. 1999. Ανακτήθηκε στις 17 Ιουνίου 2012.
- ↑ Jones R. & Wykes C.: Holographic and Speckle Interferometry, Cambridge University Press, 1989
- ↑ Butters, J.N.; Leendertz, J.A. (1971). «A double exposure technique for speckle pattern interferometry». Journal of Physics E: Scientific Instruments 4 (4): 277-279. doi:. Bibcode: 1971JPhE....4..277B.
- ↑ Dvořáková, P.; Bajgar, V.; Trnka, J. (2007). «Dynamic Electronic Speckle Pattern Interferometry in Application to Measure Out-Of-Plane Displacement». Engineering Mechanics 14 (1/2): 37-44. http://www.im.fme.vutbr.cz/pdf/14_1_037.pdf.
- ↑ Moustafa, N.A.; Hendawi, N. (2003). «Comparative Phase-Shifting Digital Speckle Pattern Interferometry Using Single Reference Beam Technique». Egypt. J. Sol. 26 (2): 225-229. doi:. http://egmrs.powweb.com/EJS/PDF/vo262/225.pdf. Ανακτήθηκε στις 22 May 2012.
- ↑ Buga, A.· Jokela, J.· Putrimas, R. «Traceability, stability and use of the Kyviskes calibration baseline–the first 10 years» (PDF). Environmental Engineering, The 7th International Conference. Vilnius Gediminas Technical University. σελίδες 1274–1280. Ανακτήθηκε στις 9 Απριλίου 2012.[νεκρός σύνδεσμος]
- ↑ Nolte, David D. (2012). Optical Interferometry for Biology and Medicine. Springer. Bibcode:2012oibm.book.....N. ISBN 978-1-4614-0889-5.
- ↑ Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T. και άλλοι. (1991). «Optical Coherence Tomography». Science 254 (5035): 1178-1181. doi:. PMID 1957169. PMC 4638169. Bibcode: 1991Sci...254.1178H. http://stuff.mit.edu:8001/afs/athena/course/2/2.717/OldFiles/www/oct_fujimoto_91.pdf. Ανακτήθηκε στις 10 April 2012.
- ↑ Fercher, A.F. (1996). «Optical Coherence Tomography». Journal of Biomedical Optics 1 (2): 157-173. doi:. PMID 23014682. Bibcode: 1996JBO.....1..157F. Αρχειοθετήθηκε από το πρωτότυπο στις 2018-09-25. https://web.archive.org/web/20180925131609/http://otg.downstate.edu/downloads/2008/spring08/refsbmi/oct/fercher.pdf. Ανακτήθηκε στις 10 April 2012.
- ↑ Lang, Walter. «Nomarski Differential Interference-Contrast Microscopy» (PDF). Carl Zeiss, Oberkochen. Ανακτήθηκε στις 10 Απριλίου 2012.
- ↑ Wax, A.; Pyhtila, J.W.; Graf, R.N.; Nines, R.; Boone, C.W.; Dasari, R.R.; Feld, M.S.; Steele, V.E. και άλλοι. (2005). «Prospective grading of neoplastic change in rat esophagus epithelium using angle-resolved low-coherence interferometry». Journal of Biomedical Optics 10 (5): 051604. doi:. PMID 16292952. Bibcode: 2005JBO....10e1604W.
- ↑ Pyhtila, J.W.; Chalut, K.J.; Boyer, J.D.; Keener, J.; d'Amico, T.; Gottfried, M.; Gress, F.; Wax, A. (2007). «In situ detection of nuclear atypia in Barrett's esophagus by using angle-resolved low-coherence interferometry». Gastrointestinal Endoscopy 65 (3): 487-491. doi:. PMID 17321252.
- ↑ Fitzgerald, Richard (2000). «Phase-sensitive x-ray imaging». Physics Today 53 (7): 23-26. doi:. Bibcode: 2000PhT....53g..23F.
- ↑ 103,0 103,1 David, C.; Nohammer, B.; Solak, H.H.; Ziegler E. (2002). «Differential x-ray phase contrast imaging using a shearing interferometer». Applied Physics Letters 81 (17): 3287-3289. doi:. Bibcode: 2002ApPhL..81.3287D.
- ↑ Wilkins, S.W.; Gureyev, T.E.; Gao, D.; Pogany, A; Stevenson, A.W. (1996). «Phase-contrast imaging using polychromatic hard X-rays». Nature 384 (6607): 335-338. doi:. Bibcode: 1996Natur.384..335W.
- ↑ Miao, Houxun; Panna, Alireza; Gomella, Andrew A.; Bennett, Eric E.; Znati, Sami; Chen, Lei; Wen, Han (2016). «A universal moiré effect and application in X-ray phase-contrast imaging». Nature Physics 12 (9): 830-834. doi:. PMID 27746823. Bibcode: 2016NatPh..12..830M.
- ↑ Davis, T.J.; Gao, D.; Gureyev, T.E.; Stevenson, A.W.; Wilkins, S.W. (1995). «Phase-contrast imaging of weakly absorbing materials using hard X-rays». Nature 373 (6515): 595-598. doi:. Bibcode: 1995Natur.373..595D.
- ↑ Momose, A.; Takeda, T.; Itai, Y.; Hirano, K. (1996). «Phase-contrast X-ray computed tomography for observing biological soft tissues». Nature Medicine 2 (4): 473-475. doi:. PMID 8597962.
- Πολυμέσα σχετικά με το θέμα Interferometry στο Wikimedia Commons