Μοναδιαία σφαίρα
Στα μαθηματικά, η μοναδιαία σφαίρα είναι μια σφαίρα μοναδιαίας ακτίνας, δηλαδή είναι το σύνολο των σημείων που έχουν Ευκλείδεια απόσταση 1 από κάποιο κέντρο στον τρισδιάστατο χώρο. Γενικότερα, η μοναδιαία -σφαίρα είναι μια -σφαίρα μοναδιαίας ακτίνας σε έναν Ευκλείδειο χώρο διαστάσεων. Ο μοναδιαίος κύκλος είναι μια ειδική περίπτωση μοναδιαίας σφαίρας: είναι η μοναδιαία -σφαίρα στο επίπεδο. Μια (ανοιχτή) μοναδιαία μπάλα είναι η περιοχή μέσα σε μια μοναδιαία σφαίρα στην οποία το σύνολο των σημείων έχουν απόσταση μικρότερη από 1 (από το κέντρο).
Μια σφαίρα ή μπάλα με μοναδιαία ακτίνα και κέντρο την αρχή των αξόνων ονομάζεται μοναδιαία σφαίρα ή μοναδιαία μπάλα. Οποιαδήποτε αυθαίρετη σφαίρα μπορεί να μετατραπεί στη μοναδιαία σφαίρα, επομένως η μελέτη των σφαιρών μπορεί συχνά να περιοριστεί στη μελέτη της μοναδιαίας σφαίρας.
Η μοναδιαία σφαίρα χρησιμοποιείται συχνά ως μοντέλο για τη σφαιρική γεωμετρία επειδή έχει σταθερή καμπυλότητα τομής ίση με 1, η οποία απλοποιεί τους υπολογισμούς. Στην τριγωνομετρία, το μήκος τόξου στον μοναδιαίο κύκλο ονομάζεται ακτίνιο και χρησιμοποιείται για τη μέτρηση της γωνιακής απόστασης. Στην σφαιρική τριγωνομετρία, το εμβαδόν της επιφάνειας στη μοναδιαία σφαίρα ονομάζεται στερακτίνιο και χρησιμοποιείται για τη μέτρηση της στερεάς γωνίας.
Σε γενικότερα πλαίσια, μια μοναδιαία σφαίρα είναι το σύνολο των σημείων που έχουν απόσταση 1 από ένα σταθερό κεντρικό σημείο, όπου μπορούν να χρησιμοποιηθούν διαφορετικές νόρμες ως γενικές έννοιες της "απόστασης", και μια (ανοικτή) μοναδιαία μπάλα βρίσκεται μέσα σε αυτό.
Μοναδιαίες σφαίρες και μπάλες στον Ευκλείδειο χώρο
ΕπεξεργασίαΣτον Ευκλείδειο χώρο με διαστάσεις, η -διάστατη μοναδιαία σφαίρα είναι το σύνολο όλων των σημείων που ικανοποιούν την εξίσωση
Η ανοιχτή μοναδιαία -μπάλα είναι το σύνολο όλων των σημείων που ικανοποιούν την ανισότητα
και η κλειστή μοναδιαία -μπάλα είναι το σύνολο όλων των σημείων που ικανοποιούν την ανισότητα
Όγκος και εμβαδόν
ΕπεξεργασίαΗ κλασσική εξίσωση μιας μοναδιαίας σφαίρας είναι αυτή ενός ελλειψοειδούς με ακτίνα 1 και χωρίς αλλαγές στους άξονες , και :
Ο όγκος της μοναδιαίας μπάλας στον Ευκλείδειο -χώρο και το εμβαδόν της επιφάνειας της μοναδιαίας σφαίρας εμφανίζονται σε πολλούς σημαντικούς τύπους στην ανάλυση. Ο όγκος της μοναδιαίας -μπάλας, που συμβολίζεται με μπορεί να εκφραστεί χρησιμοποιώντας τη συνάρτηση γάμμα. Είναι:
όπου είναι το διπλό παραγοντικό.
Ο υπερόγκος της -διάστατης μοναδιαίας σφαίρας (δηλαδή το "εμβαδόν" του συνόρου της -διάστατης μοναδιαίας μπάλας), τον οποίο συμβολίζουμε με μπορεί να εκφραστεί ως εξής:
Για παράδειγμα, είναι το "εμβαδόν" του συνόρου της μοναδιαίας μπάλας , το οποίο απλά μετράει τα δύο σημεία. είναι το "εμβαδόν" του συνόρου του μοναδιαίου δίσκου, το οποίο είναι η περιφέρεια του μοναδιαίου κύκλου. είναι το εμβαδόν του συνόρου της μοναδιαίας μπάλας , το οποίο είναι το εμβαδόν της επιφάνειας της μοναδιαίας σφαίρας .
Τα εμβαδά επιφανειών και οι όγκοι για ορισμένες τιμές του έχουν ως εξής:
| (εμβαδόν επιφάνειας) | (όγκος) | |||
|---|---|---|---|---|
| 0 | 1 | |||
| 1 | 2 | 2 | ||
| 2 | 6.283 | 3.141 | ||
| 3 | 12.57 | 4.189 | ||
| 4 | 19.74 | 4.935 | ||
| 5 | 26.32 | 5.264 | ||
| 6 | 31.01 | 5.168 | ||
| 7 | 33.07 | 4.725 | ||
| 8 | 32.47 | 4.059 | ||
| 9 | 29.69 | 3.299 | ||
| 10 | 25.50 | 2.550 | ||
Αναδρομή
ΕπεξεργασίαΟι τιμές του ικανοποιούν την αναδρομική εξίσωση:
- για .
Οι τιμές του ικανοποιούν την αναδρομική εξίσωση:
- για .
Μη αρνητικές διαστάσεις πραγματικών τιμών
ΕπεξεργασίαΗ τιμή , σε μη αρνητικές πραγματικές τιμές του , μερικές φορές χρησιμοποιείται για την κανονικοποίηση του μέτρου Χάουσντορφ.[1][2]
Άλλες ακτίνες
ΕπεξεργασίαΤο εμβαδόν επιφάνειας μιας -σφαίρας με ακτίνα είναι και ο όγκος μιας -μπάλας με ακτίνα είναι . Για παράδειγμα, το εμβαδόν είναι για τη δισδιάστατη επιφάνεια της τρισδιάστατης μπάλας ακτίνας και ο όγκος της είναι .
Μοναδιαίες μπάλες σε νορμικούς διανυσματικούς χώρους
ΕπεξεργασίαΗ ανοιχτή μοναδιαία μπάλα ενός νορμικού διανυσματικού χώρου με την νόρμα δίνεται ως το σύνολο:
- .
Είναι το (τοπολογικό) εσωτερικό της κλειστής μοναδιαίας μπάλας του
Το τελευταίο είναι η ξένη ένωση του πρώτου και το κοινό τους σύνορο, η μοναδιαία σφαίρα του , είναι:
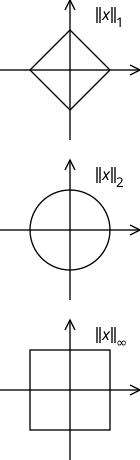
Το "σχήμα" της μοναδιαίας μπάλας εξαρτάται εξ ολοκλήρου από την επιλεγμένη νόρμα. Μπορεί κάλλιστα να έχει "γωνίες" και, για παράδειγμα, μπορεί να μοιάζει με το στην περίπτωση της μέγιστης νόρμας στον .
Έστω Ορίζουμε την συνήθης -νόρμα για ως εξής:
Τότε, το είναι η συνήθης νόρμα στον χώρο Χίλμπερτ. Το ονομάζεται κανόνας Hamming, ή -κανόνας. Η συνθήκη είναι απαραίτητη στον ορισμό της νόρμας , καθώς η μοναδιαία μπάλα σε οποιονδήποτε νορμικό χώρο πρέπει να είναι κυρτή ως συνέπεια της τριγωνικής ανισότητας. Έστω η μέγιστη νόρμα ή η -νόρμα του .
Παρατηρήστε ότι για τις μονοδιάστατες περιφέρειες από τις δισδιάστατες μοναδιαίες μπάλες, έχουμε ότι:
- είναι η ελάχιστη τιμή.
- είναι η μέγιστη τιμή.
Γενικεύσεις
ΕπεξεργασίαΜετρικοί χώροι
ΕπεξεργασίαΚαι οι τρεις παραπάνω ορισμοί μπορούν να γενικευτούν σε έναν μετρικό χώρο, εφοδιασμένο με μια επιλεγμένη αρχή των αξόνων. Ωστόσο, οι τοπολογικές ιδιότητες (εσωτερικό, κλειστότητα, σύνορο κ.τ.λ.) δεν χρειάζεται να ισχύουν με τον ίδιο τρόπο (π.χ. σε υπερμετρικούς χώρους και τα τρία είναι ταυτόχρονα ανοιχτά και κλειστά σύνολα) και η μοναδιαία σφαίρα μπορεί ακόμη και να είναι άδεια σε ορισμένους μετρικούς χώρους.
Δείτε επίσης
ΕπεξεργασίαΣημειώσεις και παραπομπές
Επεξεργασία- ↑ The Chinese University of Hong Kong, Math 5011, Chapter 3, Lebesgue and Hausdorff Measures
- ↑ Manin, Yuri I. (2006). «The notion of dimension in geometry and algebra». Bulletin of the American Mathematical Society 43 (2): 139–161. doi:. https://www.ams.org/bull/2006-43-02/S0273-0979-06-01081-0/S0273-0979-06-01081-0.pdf. Ανακτήθηκε στις 17 Δεκεμβρίου 2021.
- Mahlon M. Day (1958) Νορμικοί Γραμμικοί Χώροι, σελίδα 24, Springer-Verlag.
Εξωτερικοί σύνδεσμοι
Επεξεργασία- Weisstein, Eric W., "Μοναδιαία σφαίρα" από το MathWorld.


