Θεώρημα διχοτόμου

Στην γεωμετρία, το θεώρημα διχοτόμου (ή αλλιώς θεώρημα εσωτερικής διχοτόμου ή πρώτο θεώρημα διχοτόμου) λέει ότι σε ένα τρίγωνο η διχοτόμος μίας κορυφής του χωρίζει την απέναντι πλευρά σε δύο τμήματα με λόγο ανάλογο των δύο άλλων πλευρών.

Η εσωτερική διχοτόμος ${\rm {A\Delta }}$ της κορυφής ${\rm {A}}$ στο τρίγωνο ${\rm {AB\Gamma }}$ χωρίζει την ${\rm {B\Gamma }}$ με λόγο ${\tfrac {\rm {B\Delta }}{\rm {\Gamma \Delta }}}={\tfrac {\rm {AB}}{\rm {A\Gamma }}}$.

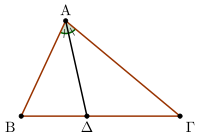
Πιο συγκεκριμένα, σε ένα τρίγωνο ${\rm {AB\Gamma }}$ αν ${\rm {A\Delta }}$ διχοτόμος, τότε

${\frac {\rm {B\Delta }}{\rm {\Gamma \Delta }}}={\frac {\rm {AB}}{\rm {A\Gamma }}}.$

Η εξωτερική διχοτόμος $\mathrm {A\Delta '}$ της κορυφής $\mathrm {A}$ στο τρίγωνο $\mathrm {AB\Gamma }$, ικανοποιεί ${\tfrac {\mathrm {B\Delta '} }{\mathrm {\Gamma \Delta '} }}={\tfrac {\mathrm {AB} }{\mathrm {A\Gamma } }}$.

Το δεύτερο θεώρημα διχοτόμου (ή θεώρημα εξωτερικής διχοτόμου) λέει ότι σε ένα τρίγωνο $\mathrm {AB\Gamma }$ με ${\rm {AB\neq {\rm {A\Gamma }}}}$ αν ${\rm {A\Delta '}}$ η εξωτερική διχοτόμος, τότε

${\frac {\rm {B\Delta '}}{\rm {\Gamma \Delta '}}}={\frac {\rm {AB}}{\rm {A\Gamma }}}.$

Αποδείξεις

Απόδειξη με θεώρημα Θαλή  

Θεωρούμε την παράλληλη ευθεία από την κορυφή ${\rm {B}}$ στην ${\rm {A\Delta }}$, που τέμνει την προέκταση της ${\rm {A\Gamma }}$ στο σημείο ${\rm {E}}$.

Από την παραλληλία, προκύπτει ότι ${\widehat {\rm {BEA}}}={\widehat {\rm {\Delta A\Gamma }}}={\tfrac {1}{2}}{\hat {\rm {A}}}$ (ως εντός-εκτός επί τα αυτά) και ${\widehat {\rm {ABE}}}={\widehat {\rm {BA\Delta }}}={\tfrac {1}{2}}{\hat {\rm {A}}}$ (ως εντός εναλλάξ). Επομένως,

${\widehat {\rm {BEA}}}={\widehat {\rm {ABE}}}$,

και άρα το τρίγωνο ${\rm {ABE}}$ είναι ισοσκελές με ${\rm {AE=AB}}$.

Τέλος, από το θεώρημα τομής του Θαλή για τις παράλληλες ${\rm {A\Delta }}$ και ${\rm {BE}}$, έχουμε ότι:

${\frac {\rm {B\Delta }}{\rm {\Gamma \Delta }}}={\frac {\rm {AE}}{\rm {A\Gamma }}}\Rightarrow {\frac {\rm {B\Delta }}{\rm {\Gamma \Delta }}}={\frac {\rm {AB}}{\rm {A\Gamma }}}$.

$\square$

Απόδειξη με τύπο για τα εμβαδά  

Σχήμα απόδειξης για το πρώτο θεώρημα διχοτόμων με εμβαδά.

Θα χρησιμοποιήσουμε τους εξής δύο τύπους για το εμβαδόν τριγώνου:

${\begin{aligned}\mathrm {E} &={\frac {1}{2}}\cdot ({\text{βάση}})\cdot ({\text{ύψος}})\\&={\frac {1}{2}}\cdot ({\text{πρώτη πλευρά }})\cdot ({\text{δεύτερη πλευρά}})\cdot \sin({\text{μεταξύ τους γωνία}}).\end{aligned}}$

Παρατηρήστε ότι τα τρίγωνα ${\rm {A\Delta B}}$ και ${\rm {A\Delta \Gamma }}$ έχουν κοινό ύψος το ${\rm {AH}}$. Επομένως τα εμβαδά τους δίνονται από

${\rm {E}}_{\rm {A\Delta B}}={\frac {1}{2}}\cdot {\rm {A\Delta }}\cdot {\rm {AB}}\cdot \sin {\tfrac {\hat {\rm {A}}}{2}}={\frac {1}{2}}\cdot {\rm {B\Delta }}\cdot {\rm {AH}}$,

και

${\rm {E}}_{\rm {A\Delta \Gamma }}={\frac {1}{2}}\cdot {\rm {A\Delta }}\cdot {\rm {A\Gamma }}\cdot \sin {\tfrac {\hat {\rm {A}}}{2}}={\frac {1}{2}}\cdot {\rm {\Gamma \Delta }}\cdot {\rm {AH}}$.

Διαιρώντας κατά μέλη αυτές τις δύο ισότητες λαμβάνουμε την ζητούμενη σχέση:

${\frac {\rm {AB}}{\rm {A\Gamma }}}={\frac {\rm {B\Delta }}{\rm {\Gamma \Delta }}}$.$\quad \square$

Πορίσματα

Το θεώρημα της διχοτόμου χρησιμοποιείται στις αποδείξεις πολλών άλλων θεωρημάτων και μετρικών σχέσεων στην γεωμετρία. Παρακάτω παραθέτουμε μερικές από αυτές.

Διχοτόμοι τριγώνου συντρέχουν

Έγκεντρο ${\rm {I}}$ του τριγώνου ${\rm {AB\Gamma }}$.

Σε ένα τρίγωνο ${\rm {AB\Gamma }}$ οι διχοτόμοι ${\rm {A\Delta _{A}}}$, ${\rm {B\Delta _{B}}}$ και ${\rm {\Gamma \Delta _{\Gamma }}}$ διέρχονται από το ίδιο σημείο (το ονομαζόμενο έγκεντρο του τριγώνου).

Απόδειξη  

Χρησιμοποιώντας το αντίστροφο του θεωρήματος του Τσέβα έχουμε ότι οι διχοτόμοι συντρέχουν, καθώς

${\frac {\mathrm {B\Delta _{A}} }{\mathrm {\Gamma \Delta _{A}} }}\cdot {\frac {\mathrm {\Gamma \Delta _{B}} }{\mathrm {A\Delta _{B}} }}\cdot {\frac {\mathrm {A\Delta _{\Gamma }} }{\mathrm {B\Delta _{\Gamma }} }}={\frac {\mathrm {AB} }{\mathrm {A\Gamma } }}\cdot {\frac {\mathrm {B\Gamma } }{\mathrm {AB} }}\cdot {\frac {\mathrm {A\Gamma } }{\mathrm {B\Gamma } }}=1$.

$\square$

Υπολογισμός ΒΔ και ΓΔ

Έστω $\alpha =\mathrm {B\Gamma }$, $\beta =\mathrm {\Gamma A}$ και $\gamma =\mathrm {AB}$, τότε

$\mathrm {B\Delta } ={\frac {\alpha \gamma }{\beta +\gamma }}$ και $\mathrm {\Gamma \Delta } ={\frac {\alpha \beta }{\beta +\gamma }}$.

Απόδειξη  

Από το θεώρημα της εσωτερικής διχοτόμου έχουμε ότι

${\frac {\rm {B\Delta }}{\rm {\Gamma \Delta }}}={\frac {\gamma }{\beta }}\Rightarrow {\rm {\Gamma \Delta }}={\rm {B\Delta }}\cdot {\frac {\beta }{\gamma }},$

και επίσης ισχύει ότι ${\rm {B\Delta }}+{\rm {\Gamma \Delta }}=\alpha$. Επομένως,

${\rm {B\Delta }}+{\rm {B\Delta }}\cdot {\frac {\beta }{\gamma }}=\alpha \Rightarrow \mathrm {B\Delta } ={\frac {\alpha \gamma }{\beta +\gamma }}.$

Αντίστοιχα και για την $\mathrm {\Gamma \Delta }$.

$\square$

Συντεταγμένες για το έγκεντρο

Σε ένα τρίγωνο ${\rm {AB\Gamma }}$ το διάνυσμα του έγκεντρου δίνεται από

${\vec {\mathrm {I} }}={\frac {1}{\alpha +\beta +\gamma }}\cdot \left(\alpha \cdot {\vec {\mathrm {A} }}+\beta \cdot {\vec {\mathrm {B} }}+\gamma \cdot {\vec {\mathrm {\Gamma } }}\right)$,

όπου ${\vec {\rm {A}}},{\vec {\rm {B}}},{\vec {\rm {\Gamma }}}$ τα διανύσματα των τριών κορυφών του τριγώνου.

Απόδειξη  

Από το θεώρημα της εσωτερικής διχοτόμου και την σχέση των $\mathrm {B\Delta _{A}}$ και $\mathrm {\Gamma \Delta _{A}}$, το σημείο $\Delta _{\rm {A}}$ της διχοτόμου δίνεται από

${\vec {\rm {\Delta _{A}}}}={\vec {\rm {B}}}+{\frac {\alpha \gamma }{\beta +\gamma }}\cdot {\frac {1}{\alpha }}\cdot ({\vec {\rm {\Gamma }}}-{\vec {\rm {B}}})={\frac {1}{\beta +\gamma }}\cdot \left(\beta \cdot {\vec {\rm {B}}}+\gamma \cdot {\vec {\Gamma }}\right)$.

Επομένως, η εξίσωση της διχοτόμου $\delta _{\rm {A}}$ δίνεται από

$\delta _{\rm {A}}=\left\{t\cdot {\vec {\mathrm {A} }}+(1-t)\cdot {\frac {1}{\beta +\gamma }}\cdot \left(\beta \cdot {\vec {\rm {B}}}+\gamma \cdot {\vec {\Gamma }}\right):t\in [0,1]\right\}$.

Αντίστοιχα, και για τις άλλες διχοτόμους

$\delta _{\rm {B}}=\left\{t\cdot {\vec {\rm {B}}}+(1-t)\cdot {\frac {1}{\gamma +\alpha }}\cdot \left(\gamma \cdot {\vec {\rm {\Gamma }}}+\alpha \cdot {\vec {\rm {A}}}\right):t\in [0,1]\right\}$,

$\delta _{\rm {\Gamma }}=\left\{t\cdot {\vec {\rm {\Gamma }}}+(1-t)\cdot {\frac {1}{\alpha +\beta }}\cdot \left(\alpha \cdot {\vec {\rm {A}}}+\beta \cdot {\vec {\rm {B}}}\right):t\in [0,1]\right\}$.

Το μοναδικό σημείο που ικανοποιεί και τις τρεις εξισώσεις (για ${\textstyle t_{\rm {A}}={\frac {\alpha }{\alpha +\beta +\gamma }}}$, ${\textstyle t_{\rm {B}}={\frac {\beta }{\alpha +\beta +\gamma }}}$ και ${\textstyle t_{\rm {\Gamma }}={\frac {\gamma }{\alpha +\beta +\gamma }}}$ αντίστοιχα) είναι το σημείο

${\vec {\mathrm {I} }}={\frac {1}{\alpha +\beta +\gamma }}\cdot \left(\alpha \cdot {\vec {\mathrm {A} }}+\beta \cdot {\vec {\mathrm {B} }}+\gamma \cdot {\vec {\mathrm {\Gamma } }}\right)$.

Επομένως, αυτό είναι το έγκεντρο του τριγώνου.

Θεώρημα εξωτερικής διχοτόμου

Απόδειξη

Η απόδειξη είναι παρόμοια με αυτή της εσωτερικής διχοτόμου που χρησιμοποιεί το θεώρημα τομής του Θαλή, αλλά το σχήμα είναι διαφορετικό. Για πληρότητα, παραθέτουμε την απόδειξη παρακάτω:

Έστω ένα τρίγωνο ${\rm {AB\Gamma }}$ με ${\rm {AB<A\Gamma }}$ και έστω ${\rm {A\Delta '}}$ η εξωτερική διχοτόμος της ${\hat {\rm {A}}}$. Θεωρούμε την παράλληλη ευθεία από την κορυφή ${\rm {B}}$ στην ${\rm {A\Delta '}}$, που την ${\rm {A\Gamma }}$ στο σημείο ${\rm {E}}$.

Από την παραλληλία, προκύπτει ότι ${\widehat {\rm {BEA}}}={\widehat {{\rm {\Delta 'A}}x}}={\tfrac {1}{2}}{\hat {\rm {A}}}$ (ως εντός-εκτός επί τα αυτά) και ${\widehat {\rm {ABE}}}={\widehat {\rm {BA\Delta '}}}={\tfrac {1}{2}}{\hat {\rm {A}}}$ (ως εντός εναλλάξ). Επομένως,

${\widehat {\rm {BEA}}}={\widehat {\rm {ABE}}},$

και άρα το τρίγωνο $\mathrm {ABE}$ είναι ισοσκελές με $\mathrm {AE} =\mathrm {AB}$.

Τέλος, από το θεώρημα τομής του Θαλή για τις παράλληλες ${\rm {A\Delta '}}$ και ${\rm {BE}}$, έχουμε ότι:

${\frac {\rm {B\Delta '}}{\rm {\Gamma \Delta '}}}={\frac {\rm {AE}}{\rm {A\Gamma }}}\Rightarrow {\frac {\rm {B\Delta '}}{\rm {\Gamma \Delta '}}}={\frac {\rm {AB}}{\rm {A\Gamma }}}$.

$\square$

Υπολογισμός των ΒΔ' και ΓΔ'

Έστω $\alpha =\mathrm {B\Gamma }$, $\beta =\mathrm {\Gamma A}$ και $\gamma =\mathrm {AB}$, τότε

$\mathrm {B\Delta '} ={\frac {\alpha \gamma }{\beta -\gamma }}$ και $\mathrm {\Gamma \Delta '} ={\frac {\alpha \beta }{\beta -\gamma }}$.

Απόδειξη  

Έστω τρίγωνο ${\rm {AB\Gamma }}$ με ${\rm {AB<A\Gamma }}$. Από το θεώρημα της εξωτερικής διχοτόμου έχουμε ότι

${\frac {\rm {B\Delta '}}{\rm {\Gamma \Delta '}}}={\frac {\gamma }{\beta }}\Rightarrow {\rm {\Gamma \Delta '}}={\rm {B\Delta '}}\cdot {\frac {\beta }{\gamma }},$

και επίσης ισχύει ότι ${\rm {\Gamma \Delta '}}-{\rm {B\Delta '}}=\alpha$ (καθώς το ${\rm {\Delta '}}$ βρίσκεται προς την μεριά του ${\rm {B}}$). Επομένως,

${\rm {B\Delta '}}\cdot {\frac {\beta }{\gamma }}-{\rm {B\Delta '}}=\alpha \Rightarrow \mathrm {B\Delta '} ={\frac {\alpha \gamma }{\beta -\gamma }}.$

Αντίστοιχα και για την $\mathrm {\Gamma \Delta '}$.

$\square$

Απολλώνιος κύκλος

Ο Απολλώνιος κύκλος του ${\rm {AB}}$ για κάποιο $k>1$. Όλα τα σημεία του ${\rm {P}}$ ικανοποιούν ${\textstyle {\frac {\rm {PA}}{\rm {PB}}}=k}$.

Το θεώρημα της εσωτερικής και εξωτερικής διχοτόμου χρησιμοποιούνται για την απόδειξη ότι ο γεωμετρικός τόπος των σημείων ${\rm {P}}$ των οποίων οι αποστάσεις από δοσμένα σημεία ${\rm {A}}$ και ${\rm {B}}$, έχουν σταθερό λόγο $k\neq 1$ (δηλαδή ${\textstyle k={\frac {\rm {PA}}{\rm {PB}}}}$), είναι ένας κύκλος. Αυτός ο κύκλος λέγεται Απολλώνιος κύκλος.

Αρμονική τετράδα

Εσωτερική διχοτόμος ${\rm {A\Delta }}$ και εξωτερική διχοτόμος ${\rm {A\Delta '}}$ τριγώνου. Τα σημεία ${\rm {\Delta ,\Delta '}}$ είναι αρμονικά συζυγή των ${\rm {B,\Gamma }}$.

Από το θεώρημα της της εσωτερικής και εξωτερικής διχοτόμου προκύπτει ότι τα σημεία ${\rm {\Delta ,\Delta '}}$ είναι αρμονικά συζυγή των ${\rm {A,B}}$, καθώς

${\frac {\rm {A\Delta }}{\rm {B\Delta }}}={\frac {\rm {A\Delta '}}{\rm {B\Delta '}}}$.

Δείτε επίσης

• Διχοτόμος γωνίας
• Έγκεντρο τριγώνου
• Απολλώνιος κύκλος