Αμοιβάδα (μαθηματικά)

Στην μιγαδική ανάλυση, έναν κλάδο των μαθηματικών, η αμοιβάδα είναι ένα σύνολο που σχετίζεται με ένα πολυώνυμο σε μία ή περισσότερες μιγαδικές μεταβλητές. Οι αμοιβάδες έχουν εφαρμογές στην αλγεβρική γεωμετρία, ιδίως στην τροπική γεωμετρία.

Η αμοιβάδα της $P(z,w)=w-2z-1.$

Η αμοιβάδα της $P(z,w)=3z^{2}+5zw+w^{3}+1.$ Σημειώστε το "κενό" στη μέση της αμοιβάδας.

Η αμοιβάδα της $P(z,w)=1+z+z^{2}+z^{3}+z^{2}w^{3}+10zw+12z^{2}w+10z^{2}w^{2}.$

Η αμοιβάδα της $P(z,w)=50z^{3}+83z^{2}w+24zw^{2}+w^{3}+392z^{2}+414zw+50w^{2}-28z+59w-100.$

Σημεία στην αμοιβάδα της $P(x,y,z)=x+y+z-1.$ Σημειώστε ότι η αμοιβάδα είναι στην πραγματικότητα τρισδιάστατη και όχι επίπεδη (αυτό δεν είναι απολύτως εμφανές από την εικόνα).

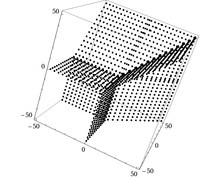
Ορισμός

Έστω η συνάρτηση

$\operatorname {Log} :{\big (}{\mathbb {C} }\setminus \{0\}{\big )}^{n}\to \mathbb {R} ^{n}$

που ορίζεται στο σύνολο όλων των n-tuples $z=(z_{1},z_{2},\dots ,z_{n})$ μη μηδενικών μιγαδικών αριθμών με τιμές στον Ευκλείδειο χώρο $\mathbb {R} ^{n},$ που δίνεται από τον τύπο

$\operatorname {Log} (z_{1},z_{2},\dots ,z_{n})={\big (}\log |z_{1}|,\log |z_{2}|,\dots ,\log |z_{n}|{\big )}.$

Εδώ, το log δηλώνει τον φυσικό λογάριθμο. Αν p(z) είναι ένα πολυώνυμο σε $n$ μιγαδικές μεταβλητές, η αμοιβάδα του ${\mathcal {A}}_{p}$ ορίζεται ως η εικόνα του συνόλου των μηδενικών του p υπό Log, οπότε

${\mathcal {A}}_{p}=\left\{\operatorname {Log} (z):z\in {\big (}\mathbb {C} \setminus \{0\}{\big )}^{n},p(z)=0\right\}.$

Οι αμοιβάδες παρουσιάστηκαν το 1994 σε ένα βιβλίο των Γκελφάντ, Καπράνοφ και Ζελεβίνσκι.

Ιδιότητες

Έστω $V\subset (\mathbb {C} ^{*})^{n}$ ο μηδενικός τόπος ενός πολυωνύμου

$f(z)=\sum _{j\in A}a_{j}z^{j}$

όπου $A\subset \mathbb {Z} ^{n}$ είναι πεπερασμένο, $a_{j}\in \mathbb {C}$ και $z^{j}=z_{1}^{j_{1}}\cdots z_{n}^{j_{n}}$ αν $z=(z_{1},\dots ,z_{n})$ και $j=(j_{1},\dots ,j_{n})$. Έστω $\Delta _{f}$ το πολύεδρο του Νεύτων της $f$, i.e., δηλ,

$\Delta _{f}={\text{Convex Hull}}\{j\in A\mid a_{j}\neq 0\}.$

Τότε

• Κάθε αμοιβάδα είναι ένα κλειστό σύνολο.
• Κάθε συνδεδεμένη συνιστώσα του συμπληρώματος $\mathbb {R} ^{n}\setminus {\mathcal {A}}_{p}$ είναι κυρτό.
• Το εμβαδόν μιας αμοιβάδας ενός μη πανομοιότυπα μηδενικού πολυωνύμου σε δύο μιγαδικές μεταβλητές είναι πεπερασμένο.
• Μια δισδιάστατη αμοιβάδα διαθέτει έναν αριθμό "πλοκαμιών", που είναι απείρως μακριά και εκθετικά στενότερα προς το άπειρο.
• Ο αριθμός των συνδεδεμένων συνιστωσών του συμπληρώματος $\mathbb {R} ^{n}\setminus {\mathcal {A}}_{p}$ δεν είναι μεγαλύτερος από $\#(\Delta _{f}\cap \mathbb {Z} ^{n})$ και όχι μικρότερος από τον αριθμό των κορυφών του $\Delta _{f}$.
• Υπάρχει μια έγχυση από το σύνολο των συνδεδεμένων συνιστωσών του συμπληρώματος $\mathbb {R} ^{n}\setminus {\mathcal {A}}_{p}$ στο $\Delta _{f}\cap \mathbb {Z} ^{n}$. Οι κορυφές του $\Delta _{f}$ βρίσκονται στην εικόνα κάτω από αυτή την έγχυση. Μια συνδεδεμένη συνιστώσα του συμπληρώματος $\mathbb {R} ^{n}\setminus {\mathcal {A}}_{p}$ είναι περιορισμένη αν και μόνο αν η εικόνα της βρίσκεται στο εσωτερικό του $\Delta _{f}$.

Συνάρτηση Ρόνκιν

Ένα χρήσιμο εργαλείο για τη μελέτη των αμοιβάδων είναι η συνάρτηση Ρόνκιν. Για p(z), ένα πολυώνυμο σε n μιγαδικές μεταβλητές, ορίζεται η συνάρτηση Ρόνκιν

$N_{p}:\mathbb {R} ^{n}\to \mathbb {R}$

σύμφωνα με τον τύπο

$N_{p}(x)={\frac {1}{(2\pi i)^{n}}}\int _{\operatorname {Log} ^{-1}(x)}\log |p(z)|\,{\frac {dz_{1}}{z_{1}}}\wedge {\frac {dz_{2}}{z_{2}}}\wedge \cdots \wedge {\frac {dz_{n}}{z_{n}}},$

όπου $x$ denotes $x=(x_{1},x_{2},\dots ,x_{n}).$ Ισοδύναμα, το $N_{p}$ δίνεται από το ολοκλήρωμα

$N_{p}(x)={\frac {1}{(2\pi )^{n}}}\int _{[0,2\pi ]^{n}}\log |p(z)|\,d\theta _{1}\,d\theta _{2}\cdots d\theta _{n},$

όπου

$z=\left(e^{x_{1}+i\theta _{1}},e^{x_{2}+i\theta _{2}},\dots ,e^{x_{n}+i\theta _{n}}\right).$

Η συνάρτηση Ronkin είναι κυρτή και συγγενής σε κάθε συνδεδεμένη συνιστώσα του συμπληρώματος της αμοιβάδας του $p(z)$.

Ενδεικτικά, η συνάρτηση Ρόνκιν ενός μονοωνύμου

$p(z)=az_{1}^{k_{1}}z_{2}^{k_{2}}\dots z_{n}^{k_{n}}$

με $a\neq 0$ είναι

$N_{p}(x)=\log |a|+k_{1}x_{1}+k_{2}x_{2}+\cdots +k_{n}x_{n}.$

Βιβλιογραφία

• Itenberg, Ilia· Mikhalkin, Grigory· Shustin, Eugenii (2007). Tropical algebraic geometry. Oberwolfach Seminars. 35. Basel: Birkhäuser. ISBN 978-3-7643-8309-1. Zbl 1162.14300. 
• Viro, Oleg (2002), «What Is ... An Amoeba?», Notices of the American Mathematical Society 49 (8): 916–917, https://www.ams.org/notices/200208/what-is.pdf .
• Thorsten Theobald, « Computing amoebas », Exp. Math., vol. 11, 2002, p. 513–526 (DOI 10.1080/10586458.2002.10504703, (on line).
• Antoine Chambert-Loir, « Quand la géométrie devient tropicale », Pour la science, no 492, octobre 2018, p. 26-33

Δημοσιεύσεις

• texts Approximating amoebas and coamoebas by sums of squares "
• texts Amoebas, Nonnegative Polynomials and Sums of Squares Supported on Circuits
• " texts Amoebas and coamoebas of linear spaces "
• Theobald, Thorsten (2002). «Computing amoebas». Exp. Math. 11 (4): 513–526. doi:10.1080/10586458.2002.10504703. . https://eudml.org/doc/52814.