Συμπλήρωμα (θεωρία συνόλων)

Στην θεωρία συνόλων, το συμπλήρωμα ενός συνόλου $A$ είναι το σύνολο που περιέχει όλα τα στοιχεία που δεν ανήκουν στο $A$, και συμβολίζεται ως $A^{c}$ ή $A'$.

Διάγραμμα Βενν για το απόλυτο συμπλήρωμα συνόλου.

Διάγραμμα Βενν για το σχετικό συμπλήρωμα συνόλου $Y$ από το $X$.

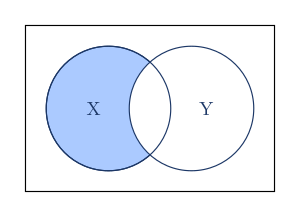
Όταν το υπερσύνολο όλων των στοιχείων $\Omega$ είναι ξεκάθαρο από τα συμφραζώμενα, τότε το απόλυτο συμπλήρωμα του $A$ είναι όλα τα στοιχεία του $\Omega$ που δεν ανήκουν στο $A$.

Το σχετικό συμπλήρωμα (ή διαφορά) του $A$ και του $B$ είναι το σύνολο που περιέχει όλα τα στοιχεία του $A$ που δεν ανήκουν στο $B$ και συμβολίζεται ως $A\setminus B$ (ή $A-B$).

Παραδείγματα

• Το απόλυτο συμπλήρωμα των φυσικών αριθμών $\mathbb {N} =\{0,1,2,\ldots \}$ είναι $\{-1,-2,-3,\ldots \}$ (όταν το $\Omega =\mathbb {Z} =\{\ldots ,-1,0,+1,\ldots \}$), ενώ περιέχει επιπλέον στοιχεία όπως $1.2,\pi ,31.5,\ldots$ όταν $\Omega =\mathbb {R}$.
• Η διαφορά των συνόλων $A=\{2,3,7,9,10,11\}$ και $B=\{3,4,7,9,11\}$ είναι το σύνολο $A\setminus B=\{2,10\}$.
• Έστω $A$ το σύνολο των γυναικών στην Ελλάδα και $B$ το σύνολο όλων των ανθρώπων κάτω των 65. Τότε η διαφορά των $A$ και $B$ είναι οι ηλικιωμένες γυναίκες στην Ελλάδα.

Απόλυτο συμπλήρωμα

Το απόλυτο συμπλήρωμα του $A$ είναι το σύνολο

$A^{c}=\{x\in \Omega :x\notin A\}$.

Ιδιότητες

Για κάθε σύνολο $A$ και $B$ ισχύει ότι:

• $A\cup A^{c}=\Omega$.
• $A\cap A^{c}=\varnothing$.
• $(A^{c})^{c}=A$.
• $A\subseteq B$ ανν $B^{c}\subseteq A^{c}$.
• $(A\cap B)^{c}=A^{c}\cup B^{c}$ (Τύποι Ντε Μόργκαν).
• $(A\cup B)^{c}=A^{c}\cap B^{c}$ (Τύποι Ντε Μόργκαν)
• $(A\times B)^{c}=(A^{c}\times B^{c})\cup (A^{c}\times B)\cup (A\times B^{c})$.

Σχετικό συμπλήρωμα (ή διαφορά συνόλων)

Το σχετικό συμπλήρωμα (ή διαφορά) του $A$ και του $B$ είναι το σύνολο που περιέχει όλα τα στοιχεία του $A$ που δεν ανήκουν στο $B$, δηλαδή το σύνολο

$A\setminus B=\{x\in A:x\notin B\}$.

Επομένως το απόλυτο συμπλήρωμα $A^{c}=\Omega \setminus A$ και η διαφορά $A\setminus B=A\cap B^{c}$.

Ιδιότητες

Για κάθε σύνολο $A,B,C,D$ ισχύει ότι:

• $A\setminus A=\varnothing$.
• $A\setminus \varnothing =A$.
• $\varnothing \setminus A=\varnothing$.
• $A\setminus B=(A\cup B)\setminus B=A\setminus (A\cap B)$.
• $(A\setminus B)\cap B=\varnothing$.
• $A\subseteq B$ ανν $A\setminus B=\emptyset$.
• $(A\setminus B)\times C=(A\times C)\setminus (B\times C)$ (επιμεριστική ιδιότητα).
• $(A\setminus B)\times (C\setminus D)=(A\times C)\cap (B^{c}\times D^{c})$.
• $(C\times D)\setminus (A\times B)=((C-A)\times D)\cup (C\times (D-B))$.

Δείτε επίσης

• Ένωση συνόλων
• Τομή συνόλων
• Παράδοξο Russell