Κυκλική τομή
Στη γεωμετρία, μια κυκλική τομή[1] είναι ένας κύκλος σε μια δευτεροβάθμια επιφάνεια (όπως ένα ελλειψοειδές ή ένα υπερβολοειδές). Είναι μια ειδική επίπεδη τομή της δευτεροβάθμιας, καθώς ο κύκλος αυτός είναι η τομή με τη δευτεροβάθμια του επιπέδου που περιέχει τον κύκλο.
Κάθε επίπεδη τομή μιας σφαίρας είναι κυκλική τομή, αν περιέχει τουλάχιστον 2 σημεία. Κάθε δευτεροβάθμια της περιστροφής περιέχει κύκλους ως τμήματα με επίπεδα που είναι ορθογώνια στον άξονά της- δεν περιέχει άλλους κύκλους, αν δεν είναι σφαίρα. Περισσότερο κρυμμένοι είναι οι κύκλοι σε άλλα δευτεροβάθμια, όπως τα τριαξονικά ελλειψοειδή, οι ελλειπτικοί κύλινδροι κ.λπ. Παρ' όλα αυτά, είναι γεγονός ότι:
- Κάθε δευτεροβάθμια επιφάνεια που περιέχει ελλείψεις περιέχει και κύκλους.
Αν μια δευτεροβάθμια περιέχει έναν κύκλο, τότε κάθε τομή της δευτεροβάθμιας με ένα επίπεδο παράλληλο σε αυτόν τον κύκλο είναι επίσης κύκλος, με την προϋπόθεση ότι περιέχει τουλάχιστον δύο σημεία. Εκτός από τις σφαίρες, οι κύκλοι που περιέχονται σε ένα τετράγωνο, αν υπάρχουν, είναι όλοι παράλληλοι σε ένα από τα δύο σταθερά επίπεδα (τα οποία είναι ίσα στην περίπτωση ενός τετραγώνου περιστροφής).
Οι κυκλικές τομές χρησιμοποιούνται στην κρυσταλλογραφία.[2][3][4]
Χρησιμοποιώντας την προβολική γεωμετρία
ΕπεξεργασίαΤα κυκλικά τμήματα μιας δευτεροβάθμιας μπορούν να υπολογιστούν από την έμμεση εξίσωση της τετραγωνικής, όπως γίνεται στις επόμενες ενότητες. Μπορούν επίσης να χαρακτηριστούν και να μελετηθούν με τη χρήση συνθετικής προβολικής γεωμετρίας.
Έστω C η τομή μιας τετραγωνικής επιφάνειας Q και ενός επιπέδου P. Σε αυτή την ενότητα, Q και C είναι επιφάνειες στον τρισδιάστατο Ευκλείδειο χώρο, οι οποίες επεκτείνονται στον προβολικό χώρο πάνω στους μιγαδικούς αριθμούς. Κάτω από αυτές τις υποθέσεις, η καμπύλη C είναι κύκλος αν και μόνο αν η τομή της με το επίπεδο στο άπειρο περιλαμβάνεται στην ομβίλη (η καμπύλη στο άπειρο της εξίσωσης ).
Η πρώτη περίπτωση που πρέπει να εξεταστεί είναι όταν η τομή του Q με το επίπεδο στο άπειρο αποτελείται από μία ή δύο πραγματικές γραμμές, δηλαδή όταν το Q είναι είτε ένα υπερβολικό παραβολοειδές, είτε ένας παραβολικός κύλινδρος, είτε ένας υπερβολικός κύλινδρος. Στην περίπτωση αυτή τα σημεία στο άπειρο του C είναι πραγματικά (τομή πραγματικού επιπέδου με πραγματικές ευθείες). Συνεπώς, οι επίπεδες τομές του Q δεν μπορούν να είναι κύκλοι (ούτε ελλείψεις).
Αν Q είναι μια σφαίρα, η τομή της με το επίπεδο στο άπειρο είναι η ομφαλική, και όλες οι επίπεδες τομές είναι κύκλοι.
Αν Q είναι μια επιφάνεια περιστροφής, η τομή της με την ομφαλική αποτελείται από ένα ζεύγος μιγαδικών συζυγών σημείων (τα οποία είναι διπλά σημεία). Ένα πραγματικό επίπεδο περιέχει αυτά τα δύο σημεία αν και μόνο αν είναι κάθετο στον άξονα της περιστροφής. Έτσι οι κυκλικές τομές είναι οι τομές του επιπέδου από ένα επίπεδο κάθετο στον άξονα, που έχουν τουλάχιστον δύο πραγματικά σημεία.
Στις υπόλοιπες περιπτώσεις, η τομή του Q με τον ομφαλό αποτελείται από δύο διαφορετικά ζεύγη μιγαδικών συζυγών σημείων. Καθώς η C είναι καμπύλη δευτέρου βαθμού, η τομή της με το επίπεδο στο άπειρο αποτελείται από δύο σημεία, ενδεχομένως ίσα. Η καμπύλη C είναι επομένως κύκλος, αν αυτά τα δύο σημεία είναι ένα από αυτά τα δύο ζεύγη μιγαδικών συζυγών σημείων του ομφαλού. Κάθε ένα από αυτά τα ζεύγη ορίζει μια πραγματική ευθεία (που διέρχεται από τα σημεία), η οποία είναι η τομή της P με το επίπεδο στο άπειρο. Έτσι, έχουμε κυκλική τομή αν και μόνο αν η C έχει τουλάχιστον δύο πραγματικά σημεία και η P περιέχει μία από αυτές τις ευθείες στο άπειρο (δηλαδή αν η P είναι παράλληλη σε μία από τις δύο κατευθύνσεις που ορίζονται από αυτές τις ευθείες στο άπειρο).
Προσδιορισμός των κυκλικών τομών μιας δευτεροβάθμιας
ΕπεξεργασίαΓια να βρούμε τα επίπεδα, τα οποία περιέχουν κυκλικές τομές μιας δεδομένης δευτεροβάθμιας, χρησιμοποιούμε τις ακόλουθες προτάσεις:
- (S:) Αν τα κοινά σημεία μιας δευτεροβάθμιας με μια σφαίρα περιέχονται σε ένα ζεύγος επιπέδων, τότε η καμπύλη τομής αποτελείται από δύο κύκλους.
- (P:) Αν η τομή ενός επιπέδου και μιας δευτεροβάθμιας είναι ένας κύκλος, τότε κάθε παράλληλο επίπεδο, που περιέχει τουλάχιστον δύο σημεία της δευτεροβάθμιας, τέμνει την δευτεροβάθμια επίσης σε κύκλο.
Επομένως, η στρατηγική για την ανίχνευση κυκλικών τομών είναι:
- 1) να βρεθεί μια σφαίρα που τέμνει τη δευτεροβάθμια σε ένα ζεύγος επιπέδων και
- 2) Τα επίπεδα που είναι παράλληλα με τα ανιχνευθέντα παραδίδουν τα υπόλοιπα κυκλικά τμήματα.
Τριαξονικό ελλειψοειδές
ΕπεξεργασίαΓια το ελλειψοειδές με εξίσωση
και τους ημιάξονες χρησιμοποιεί κανείς μια βοηθητική σφαίρα με εξίσωση
Η ακτίνα της σφαίρας πρέπει να επιλεγεί έτσι ώστε η τομή με το ελλειψοειδές να περιέχεται σε δύο επίπεδα μέσω της αρχής. Πολλαπλασιάζοντας την εξίσωση του ελλειψοειδούς με και αφαιρώντας την εξίσωση της σφαίρας προκύπτει:
Αυτή η εξίσωση περιγράφει ένα ζεύγος επιπέδων, εάν ένας από τους 3 συντελεστές είναι μηδέν. Στην περίπτωση ή η εξίσωση ικανοποιείται μόνο από τον άξονα x ή τον άξονα z. Μόνο στην περίπτωση έχουμε ένα ζεύγος επιπέδων με εξίσωση
επειδή μόνο σε αυτή την περίπτωση οι υπόλοιποι συντελεστές έχουν διαφορετικό πρόσημο (λόγω: ).
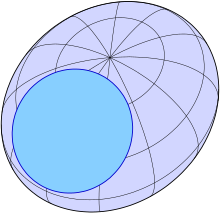
Το διάγραμμα δίνει μια εντύπωση των πιο συνηθισμένων τομών μεταξύ μιας σφαίρας και ενός ελλειψοειδούς και τονίζει την εξαιρετική κυκλική περίπτωση (μπλε).
Εάν οι τιμές των ημιάξονα πλησιάζουν, οι δύο μολύβδινες γραμμές των επιπέδων (και των κύκλων) πλησιάζουν είτε. Για όλα τα επίπεδα είναι κάθετα στον άξονα z (άξονας περιστροφής).
Απόδειξη της ιδιότητας (P)
Στρέφοντας το ελλειψοειδές γύρω από τον άξονα y έτσι ώστε ένας από τους δύο κύκλους (μπλε) να βρίσκεται στο επίπεδο x-y προκύπτει μια νέα εξίσωση του ελλειψοειδούς:
Για έχουμε , η οποία πρέπει να είναι η εξίσωση ενός κύκλου. Αυτό ισχύει μόνο αν .
Η τομή του ελλειψοειδούς με ένα επίπεδο με εξίσωση , (παράλληλο προς το επίπεδο x-y) έχει την εξίσωση
- .
Αυτή η εξίσωση περιγράφει έναν κύκλο ή ένα σημείο ή το κενό σύνολο. Το κέντρο και η ακτίνα του κύκλου μπορούν να βρεθούν συμπληρώνοντας το τετράγωνο.
Ελλειπτικό υπερβολοειδές ενός φύλλου
ΕπεξεργασίαΓια το υπερβολοειδές ενός φύλλου με εξίσωση
κατ' αναλογία παίρνουμε για την τομή με τη σφαίρα την εξίσωση
Μόνο για έχουμε ένα ζεύγος επιπέδων:
Ελλειπτικός κύλινδρος
ΕπεξεργασίαΓια τον ελλειπτικό κύλινδρο με εξίσωση
προκύπτει η εξίσωση
Μόνο για έχουμε ένα ζεύγος επιπέδων:
Ελλειπτικό παραβολοειδές
ΕπεξεργασίαΓια το ελλειπτικό παραβολοειδές με εξίσωση
επιλέγεται μια σφαίρα που περιέχει την κορυφή (αρχή) και με κέντρο τον άξονα (άξονας z) :
Μετά την εξάλειψη των γραμμικών τμημάτων προκύπτει η εξίσωση
Μόνο για έχουμε ένα ζεύγος επιπέδων :
Ελλειπτικό υπερβολοειδές δύο φύλλων
ΕπεξεργασίαΤο υπερβολοειδές δύο φύλλων με εξίσωση
μετατοπίζεται αρχικά έτσι ώστε η μία κορυφή να είναι η αρχή (βλ. διάγραμμα):
Αναλογικά με την περίπτωση του παραβολοειδούς επιλέγεται μια σφαίρα που περιέχει την αρχή με κέντρο τον άξονα z:
Μετά την εξάλειψη των γραμμικών τμημάτων προκύπτει η εξίσωση
Μόνο για έχουμε ένα ζεύγος επιπέδων:
Ελλειπτικός κώνος
ΕπεξεργασίαΟ ελλειπτικός κώνος με εξίσωση
μετατοπίζεται έτσι ώστε η κορυφή να μην είναι η αρχή (βλέπε διάγραμμα):
Τώρα είναι κατάλληλη μια σφαίρα με κέντρο την αρχή:
Η απαλοιφή του δίνει:
Στην περίπτωση αυτή η συμπλήρωση του τετραγώνου δίνει:
Για να πάρουμε την εξίσωση ενός ζεύγους επιπέδων, το δεξιό μέρος της εξίσωσης πρέπει να είναι μηδέν, πράγμα που ισχύει για
Η λύση για το z δίνει:
Δείτε επίσης
ΕπεξεργασίαΕξωτερικοί σύνδεσμοι
Επεξεργασία- English - Greek Dictionary of Pure and Applied Mathematics Εθνικό Μετσόβιο Πολυτεχνείο
- Αγγλοελληνικό Λεξικό Μαθηματικής Ορολογίας - Πανεπιστήμιο Κύπρου
- Matrix Analysis
- Coordinate Geometry for JEE Advanced, 3E (Free Sample)
- Complex Geometry: An Introduction
- The Elements Of Co-ordinate Geometry By S.L. Loney | Cartesian and Polar ...
- Nonuniform Flow Functions, Circular Section
Δημοσιεύσεις
Επεξεργασία- Μαυρογιάννης, Ν. Σ. (Μαΐου 2016). «Μία εισαγωγή στους μιγαδικούς αριθμούς». Εκθέτης Φύλλα Μαθηματικής Παιδείας (16): 1-8. http://ekthetis.gr/Ekthetis016.pdf.
- Bronshtein, I. N.· Semendyayev, K. A. (29 Ιουνίου 2013). Handbook of Mathematics. Springer Science & Business Media. ISBN 978-3-662-21982-9.
- Gray, Lawrence F.; Flanigan, Francis J.; Kazdan, Jerry L.; Frank, David H.; Fristedt, Bert (1990), Calculus two: linear and nonlinear functions, Berlin: Springer-Verlag, σελ. 375, ISBN 0-387-97388-5, https://archive.org/details/calculustwolinea00flan/page/375
- Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd έκδοση), New York, NY: Chelsea, ISBN 978-0-8284-1087-8
- von Petersdorff, Tobias (2006), «Critical Points of Autonomous Systems», Differential Equations for Scientists and Engineers (Math 246 lecture notes), https://www.math.umd.edu/~petersd/246/stab.html
- Widder, D. V. (1989), Advanced calculus, New York, NY: Dover Publications, σελ. 128, ISBN 0-486-66103-2
- H. F. Baker: Principles of Geometry, Volume 3, Cambridge University Press, 2010, ISBN 978-1-108-01779-4.
- D. M. Y. Sommerville: Analytical Geometry of Three Dimensions, Cambridge University Press, 1959, ISBN 978-1-316-60190-7, p. 204.
- K. P. Grotemeyer: Analytische Geometrie. Göschen-Verlag, 1962, p. 143.
- H. Scheid, W. Schwarz: Elemente der Linearen Algebra und der Analysis. Spektrum, Heidelberg, 2009, ISBN 978-3-8274-1971-2, p. 132.
Παραπομπές
Επεξεργασία- ↑ Station (U.S.), Waterways Experiment· Station, U. S. Army Engineer Waterways Experiment (1963). Nonuniform Flow Functions, Circular Section. U.S. Army Engineer Waterways Experiment Station, Corps of Engineers.
- ↑ W. H. Westphal: Physikalisches Wörterbuch: Zwei Teile in Einem Band. Springer-Verlag, 1952, (ISBN 978-3-662-12707-0), p. 350.
- ↑ H. Tertsch: Die Festigkeitserscheinungen der Kristalle. Springer-Verlag, Wien, 1949, (ISBN 978-3-211-80120-8), p. 87.
- ↑ G. Masing: Lehrbuch der Allgemeinen Metallkunde. Springer-Verlag, Berlin, 1950, (ISBN 978-3-642-52-993-1), p. 355.