Θεώρημα van Schooten
Στην γεωμετρία, το θεώρημα van Schooten λέει ότι για οποιοδήποτε σημείο του περιγεγραμμένου κύκλου ενός ισόπλευρου τριγώνου , ισχύει ότι η μεγαλύτερη απόσταση από τις κορυφές του ισούται με το άθροισμα των αποστάσεων του από τις άλλες δύο.[1][2]
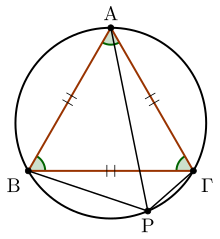
Το θεώρημα παίρνει το όνομά του από τον μαθηματικό Frans van Schooten.
Αποδείξεις
Επεξεργασία| Απόδειξη με θεώρημα Πτολεμαίου |
|
Από το Θεώρημα του Πτολεμαίου στο εγγεγραμμένο τετράπλευρο έχουμε ότι Αφού το τρίγωνο είναι ισόπλευρο έχουμε ότι . Από την προηγούμενη σχέση, καταλήγουμε ότι |
| Απόδειξη με στοιχειώδη γεωμετρία |
|
Θεωρούμε το σημείο του περιγεγραμμένου κύκλου ώστε . Τότε, ως εγγεγραμμένες γωνίες που βαίνουν στο ίδιο τόξο. Επομένως, το τρίγωνο είναι ισόπλευρο. Αντίστοιχα, και . Επομένως, το τρίγωνο είναι ισόπλευρο. Αφού και , έχουμε ότι ως χορδές στις οποίες βαίνουν σε ίσες εγγεγραμμένες γωνίες. Άρα και . Καταλήγουμε ότι |
Δείτε επίσης
ΕπεξεργασίαΕξωτερικοί σύνδεσμοι
ΕπεξεργασίαΠαραπομπές
Επεξεργασία- ↑ Viglione, Raymond (Απριλίου 2016). «Proof Without Words: van Schooten's Theorem». Mathematics Magazine 89 (2): 132–132. doi:.
- ↑ Στεργίου, Χαράλαμπος (2011). Γεωμετρία για διαγωνισμούς: Τρίγωνα, τετράπλευρα, κύκλος, εγγράψιμα. Αθήνα: Σαββάλας. ISBN 9789604930357.


