Θεώρημα Βιβιάνι

Στην γεωμετρία, το θεώρημα Βιβιάνι (αναφέρεται και ως θεώρημα Viviani) λέει ότι σε κάθε ισόπλευρο τρίγωνο $\mathrm {AB\Gamma }$ και για $\mathrm {P}$ ένα τυχόν εσωτερικό του σημείο, ισχύει ότι

Σύμφωνα με το Θεώρημα Βιβιάνι, $d_{1}+d_{2}+d_{3}=\upsilon$.

$d_{1}+d_{2}+d_{3}=\upsilon$,

όπου $d_{1},d_{2},d_{3}$ οι αποστάσεις του $\mathrm {P}$ από τις πλευρές του τριγώνου και $\upsilon$ το ύψος του τριγώνου.

Απόδειξη

Απόδειξη  

Ο χωρισμός του τριγώνου $\mathrm {AB\Gamma }$ στα επιμέρους τρίγωνα $\mathrm {APB} ,\mathrm {AP\Gamma } ,\mathrm {BP\Gamma }$.

Θα χρησιμοποιήσουμε τον εξής τύπο για το εμβαδόν ενός τριγώνου:

$\mathrm {E} ={\frac {1}{2}}\cdot ({\text{βάση}})\cdot ({\text{ύψος}}).$

Χωρίζοντας το αρχικό τρίγωνο στα τρίγωνα $\mathrm {APB} ,\mathrm {AP\Gamma } ,\mathrm {BP\Gamma }$, έχουμε ότι

$\mathrm {E} _{\mathrm {AB\Gamma } }=\mathrm {E} _{\mathrm {APB} }+\mathrm {E} _{\mathrm {AP\Gamma } }+\mathrm {E} _{\mathrm {BP\Gamma } }.$

Επομένως, αν $x$ είναι η πλευρά του ισοπλεύρου τριγώνου, τότε

${\frac {1}{2}}\cdot x\cdot \upsilon ={\frac {1}{2}}\cdot x\cdot d_{1}+{\frac {1}{2}}\cdot x\cdot d_{2}+{\frac {1}{2}}\cdot x\cdot d_{3}={\frac {1}{2}}\cdot x\cdot (d_{1}+d_{2}+d_{3}).$

Απλοποιώντας το ${\tfrac {1}{2}}x$, καταλήγουμε στην ζητούμενη έκφραση

$\upsilon =d_{1}+d_{2}+d_{3}$.

Επεκτάσεις

Για ισοσκελές τρίγωνο

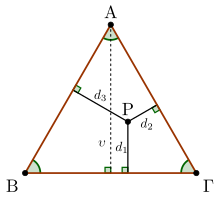
Το θεώρημα Βιβιάνι για ισοσκελή τρίγωνα.

Θεώρημα — Έστω ένα ισοσκελές τρίγωνο $\mathrm {AB\Gamma }$ με $\mathrm {AB} =\mathrm {A\Gamma }$ και ένα σημείο $\mathrm {P}$ της $\mathrm {B\Gamma }$. Αν $d_{1}$ και $d_{2}$ είναι οι αποστάσεις του $\mathrm {P}$ από τις $\mathrm {AB}$ και $\mathrm {A\Gamma }$, και $\upsilon$ το ύψος που αντιστοιχεί στην κορυφή $\mathrm {A}$, τότε

$d_{1}+d_{2}=\upsilon$.

Απόδειξη  

Έστω ένα ισοσκελές τρίγωνο $\mathrm {AB\Gamma }$ με $\mathrm {AB} =\mathrm {A\Gamma } =x$. Χωρίζοντας το στα τρίγωνα $\mathrm {ABP}$ και $\mathrm {A\Gamma P}$, έχουμε ότι

$\mathrm {E} _{\mathrm {AB\Gamma } }=\mathrm {E} _{\mathrm {ABP} }+\mathrm {E} _{\mathrm {A\Gamma P} }$.

Χρησιμοποιώντας τον τύπο για το εμβαδόν του τριγώνου έχουμε ότι

${\frac {1}{2}}x\cdot \upsilon ={\frac {1}{2}}x\cdot d_{1}+{\frac {1}{2}}x\cdot d_{2}$.

Απλοποιώντας το ${\tfrac {1}{2}}x$, λαμβάνουμε ότι

$\upsilon =d_{1}+d_{2}$.

Το θεώρημα Βιβιάνι για εξωτερικό σημείο του τριγώνου.

Για εξωτερικό σημείο

Θεώρημα — Το θεώρημα Βιβιάνι αφορά τα σημεία $\mathrm {P}$ που είναι εσωτερικά του ισόπλευρου τριγώνου $\mathrm {AB\Gamma }$. Όταν το $\mathrm {P}$ είναι εξωτερικό σημείο προς την πλευρά $\mathrm {B\Gamma }$, τότε ο τύπος αλλάζει σε

$\upsilon =d_{2}+d_{3}-d_{1}.$

Απόδειξη  

Θεωρούμε τα τρίγωνα $\mathrm {APB}$ και $\mathrm {AP\Gamma }$. Τότε,

$\mathrm {E} _{\mathrm {AB\Gamma } }=\mathrm {E} _{\mathrm {ABP} }+\mathrm {E} _{\mathrm {A\Gamma P} }-\mathrm {E} _{\mathrm {B\Gamma P} }$.

Χρησιμοποιώντας τον τύπο για το εμβαδόν τριγώνου, έχουμε ότι

${\frac {1}{2}}\cdot x\cdot \upsilon ={\frac {1}{2}}\cdot x\cdot d_{2}+{\frac {1}{2}}\cdot x\cdot d_{3}-{\frac {1}{2}}\cdot x\cdot d_{1}$.

Απλοποιώντας, λαμβάνουμε τη ζητούμενη σχέση.

Για κανονικά πολύγωνα

Θεώρημα — Έστω ένα κανονικό πολύγωνο $\mathrm {A} _{1},\ldots ,\mathrm {A} _{n}$ και ένα εσωτερικό του σημείο $\mathrm {P}$. Αν $d$ η απόσταση του περίκεντρου από τις πλευρές και $d_{1},\ldots ,d_{n}$ οι αποστάσεις του $\mathrm {P}$ από τις πλευρές $\mathrm {A} _{1}\mathrm {A} _{2},\ldots ,\mathrm {A} _{n-1}\mathrm {A} _{n},\mathrm {A} _{n}\mathrm {A} _{1}$, τότε ισχύει ότι

$d_{1}+\ldots +d_{n}=n\cdot d.$

Η γενίκευση του θεωρήματος Βιβιάνι για το τετράγωνο και το πεντάγωνο.

Απόδειξη  

Θεωρούμε τα τρίγωνα $\mathrm {A} _{1}\mathrm {P} \mathrm {A} _{2},\ldots ,\mathrm {A} _{n}\mathrm {P} \mathrm {A} _{1}$. Το εμβαδό του πολυγώνου ισούται με το άθροισμα των εμβαδόν των τριγώνων, άρα

${\tfrac {1}{2}}\cdot \mathrm {A} _{1}\mathrm {A} _{2}\cdot d_{1}+\ldots +{\tfrac {1}{2}}\cdot \mathrm {A} _{n}\mathrm {A} _{1}\cdot d_{n}={\tfrac {1}{2}}\cdot x\cdot (d_{1}+\ldots +d_{n}).$

Αντίστοιχα, για το κέντρο του περιγεγραμμένου κύκλου του πολυγώνου, οι αποστάσεις προς κάθε μία από τις πλευρές είναι $d$. Επομένως, το εμβαδόν του πολυγώνου δίνεται από τον τύπο

${\tfrac {1}{2}}\cdot x\cdot (d_{1}+\ldots +d_{n})={\tfrac {n}{2}}\cdot x\cdot d.$

Εξισώνοντας του τύπους για το εμβαδόν έχουμε ότι

$d=d_{1}+\ldots +d_{n}=n\cdot d,$

ολοκληρώνοντας την απόδειξη. $\square$

Περαιτέρω ανάγνωση

• Gueron, Shay; Tessler, Ran (2002). «The Fermat-Steiner problem». Amer. Math. Monthly 109 (5): 443–451. doi:10.2307/2695644. https://archive.org/details/sim_american-mathematical-monthly_2002-05_109_5/page/443. 
• Samelson, Hans (2003). «Proof without words: Viviani's theorem with vectors». Math. Mag. 76 (3): 225. doi:10.2307/3219327. https://archive.org/details/sim_mathematics-magazine_2003-06_76_3/page/225. 
• Chen, Zhibo; Liang, Tian (2006). «The converse of Viviani's theorem». The College Mathematics Journal 37 (5): 390–391. doi:10.2307/27646392. https://archive.org/details/sim_college-mathematics-journal_2006-11_37_5/page/390. 
• Kawasaki, Ken-Ichiroh; Yagi, Yoshihiro; Yanagawa, Katsuya (2005). «On Viviani's theorem in three dimensions». Math. Gaz. 89 (515): 283–287. doi:10.1017/S002555720017785X. https://archive.org/details/sim_mathematical-gazette_2005-07_89_515/page/283. 
• Zhou, Li (2012). «Viviani polytopes and Fermat Points». Coll. Math. J. 43 (4): 309–312. doi:10.4169/college.math.j.43.4.309. 

Δείτε επίσης

• Ισόπλευρο τρίγωνο
• Κανονικό πολύγωνο