Ευθεία Όιλερ
Στην γεωμετρία, σε κάθε τρίγωνο που δεν είναι ισόπλευρο, η ευθεία Όιλερ (αναφέρεται και ως ευθεία Euler) είναι η ευθεία πάνω στην οποία βρίσκεται το ορθόκεντρο , το βαρύκεντρο και το περίκεντρο . Επίσης, ισχύει ότι .[1]:77[2]:44-45[3]:274-278[4]:186 Στα ισόπλευρα τρίγωνα, αυτά τα τρία σημεία συμπίπτουν.
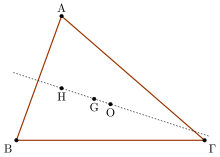
Η ευθεία αυτή περιέχει αρκετά σημεία ακόμα, όπως το κέντρο του κύκλου του Όιλερ, το σημείο Schiffler, το σημείο Exeter και το σημείο de Longchamp. Σε ένα ισόπλευρο τρίγωνο όλα αυτά τα σημεία συμπίπτουν.
Απόδειξη
Επεξεργασία| Απόδειξη |
|
Θεωρούμε το ορθόκεντρο και το βαρύκεντρο του τριγώνου, και το σημείο στην ώστε . Επίσης θεωρούμε και τα μέσα των και αντίστοιχα. Από την ιδιότητα του βαρυκέντρου να τριχοτομεί τη διάμεσο έχουμε ότι . Επομένως, από το αντίστροφο του θεωρήματος τομής του Θαλή έχουμε ότι η είναι παράλληλη στην και άρα . Άρα η είναι η μεσοκάθετος του . Αντίστοιχα, η είναι η μεσοκάθετος του και άρα είναι το περίκεντρο του τριγώνου. |
Δείτε επίσης
ΕπεξεργασίαΠαραπομπές
Επεξεργασία- ↑ Ταβανλης, Χ. Επίπεδος Γεωμετρία. Αθήνα: Ι. Χιωτελη.
- ↑ Κανελλος, Σπ. Γ. (1975). Ευκλείδειος Γεωμετρία Δ',Ε',ΣΤ' Γμνασίου Θετικής Κατευθύνσεως. Αθήνα: Οργανισμός Εκδόσεως Διδακτικών Βιβλίων. σελίδες 137–139.
- ↑ Τόγκας, Πέτρος Γ. (1957). Θεωρητική Γεωμετρία. Αθήνα: Πέτρου Γ. Τογκα. σελίδες 461–463.
- ↑ Στεργίου, Μπάμπης. Γεωμετρία για διαγωνισμούς 1: Τρίγωνα, τετράπλευρα, κύκλος, εγγράψιμα. Αθήνα: Σαββάλας. ISBN 978-960-493-035-7.
| Αυτό το λήμμα σχετικά με τη γεωμετρία χρειάζεται επέκταση. Μπορείτε να βοηθήσετε την Βικιπαίδεια επεκτείνοντάς το. |





