Στην γεωμετρία , σε ένα πολύγωνο εξωτερική γωνία είναι μία γωνία με κορυφή μία από τις κορυφές του πολυγώνου και σχηματίζεται από μία από τις πλευρές του πολυγώνου και την προέκταση της διαδοχικής της.[ 1] :23 [ 2] :55
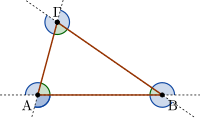
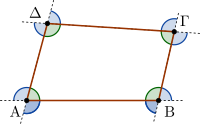
Οι εσωτερικές (πράσινες) και οι εξωτερικές (μπλε) γωνίες ενός τριγώνου και ενός τετραπλεύρου.
Σε ένα τρίγωνο η εξωτερική γωνία μίας κορυφής, ισούται με το άθροισμα των δύο άλλων κορυφών. Σε ένα τρίγωνο , η εξωτερική γωνία που αντιστοιχεί στην κορυφή
A
{\displaystyle \mathrm {A} }
180
∘
−
A
^
=
B
^
+
Γ
^
{\displaystyle 180^{\circ }-{\hat {\mathrm {A} }}={\hat {\mathrm {B} }}+{\hat {\mathrm {\Gamma } }}}
Σε ένα κυρτό πολύγωνο με
n
{\displaystyle n}
360
∘
{\displaystyle 360^{\circ }}
Απόδειξη
Αυτό προκύπτει από το γεγονός ότι το άθροισμα των γωνιών του είναι
A
^
1
+
A
^
2
+
…
+
A
^
n
=
180
∘
⋅
(
n
−
2
)
{\displaystyle {\hat {\mathrm {A} }}_{1}+{\hat {\mathrm {A} }}_{2}+\ldots +{\hat {\mathrm {A} }}_{n}=180^{\circ }\cdot (n-2)}
και επομένως, το άθροισμα των εξωτερικών γωνιών του πολυγώνου είναι ίσο με
(
180
∘
−
A
^
1
)
+
(
180
∘
−
A
^
2
)
+
…
+
(
180
∘
−
A
^
n
)
=
180
∘
⋅
n
−
(
A
^
1
+
A
^
2
+
…
+
A
^
n
)
=
180
∘
⋅
2
=
360
∘
.
{\displaystyle {\begin{aligned}&(180^{\circ }-{\hat {\mathrm {A} }}_{1})+(180^{\circ }-{\hat {\mathrm {A} }}_{2})+\ldots +(180^{\circ }-{\hat {\mathrm {A} }}_{n})\\&\quad =180^{\circ }\cdot n-({\hat {\mathrm {A} }}_{1}+{\hat {\mathrm {A} }}_{2}+\ldots +{\hat {\mathrm {A} }}_{n})\\&\quad =180^{\circ }\cdot 2\\&\quad =360^{\circ }.\end{aligned}}}
↑ Ταβανλής, Χ. Επίπεδος Γεωμετρία . Αθήνα: Ι. Χιωτελη. ↑ Παπανικολάου, Γεώργιος Χρ. (1966). Θεωρητική γεωμετρία (3η έκδοση). Αθήνα.