Στην θεωρία πιθανοτήτων και στη στατιστική , η διακριτή ομοιόμορφη κατανομή
U
{
a
,
b
}
{\displaystyle {\mathcal {U}}\{a,b\}}
{
a
,
a
+
1
,
…
,
b
}
{\displaystyle \{a,a+1,\ldots ,b\}}
[ 1] [ 2] [ 3]
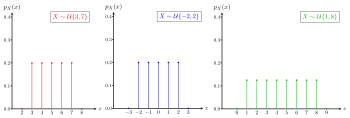
Παραδείγματα ομοιόμορφης διακριτής κατανομής. Παραδείγματα αθροιστικής κατανομής.
Διακριτή Ομοιόμορφη Κατανομή
Συμβολισμός
U
{
a
,
b
}
{\displaystyle {\mathsf {U}}\{a,b\}}
Παράμετροι
a
,
b
∈
Z
{\displaystyle a,b\in \mathbb {Z} }
b
≥
a
{\displaystyle b\geq a}
n
=
b
−
a
+
1
{\displaystyle n=b-a+1}
Φορέας
x
∈
{
a
,
a
+
1
,
…
,
b
}
{\displaystyle x\in \{a,a+1,\ldots ,b\}}
Συνάρτηση Μάζας
1
n
{\displaystyle {\frac {1}{n}}}
Μέσος
a
+
b
2
{\displaystyle {\frac {a+b}{2}}}
Διάμεσος
a
+
b
2
{\displaystyle {\frac {a+b}{2}}}
Διακύμανση
n
2
−
1
12
{\displaystyle {\frac {n^{2}-1}{12}}}
Λοξότητα
0
{\displaystyle 0}
Κύρτωση
−
6
⋅
(
n
2
+
1
)
5
⋅
(
n
2
−
1
)
−
3
{\displaystyle -{\frac {6\cdot (n^{2}+1)}{5\cdot (n^{2}-1)}}-3}
Εντροπία
log
2
n
{\displaystyle \log _{2}n}
Πιθανογεννήτρια
1
n
⋅
t
b
−
t
a
t
−
1
{\displaystyle {\frac {1}{n}}\cdot {\frac {t^{b}-t^{a}}{t-1}}}
Χαρακτηριστική
1
n
⋅
e
t
b
−
e
t
a
e
t
−
1
{\displaystyle {\frac {1}{n}}\cdot {\frac {e^{tb}-e^{ta}}{e^{t}-1}}}
Για παράδειγμα, η ρίψη ενός αμερόληπτου ζαριού μοντελοποιείται ως
U
{
1
,
6
}
{\displaystyle {\mathcal {U}}\{1,6\}}
{
1
,
2
,
3
,
4
,
5
,
6
}
{\displaystyle \{1,2,3,4,5,6\}}
1
/
6
{\displaystyle 1/6}
U
{
0
,
1
}
{\displaystyle {\mathcal {U}}\{0,1\}}
Η συνάρτηση μάζας πιθανότητας της
X
∼
U
{
a
,
b
}
{\displaystyle X\sim {\mathcal {U}}\{a,b\}}
p
X
(
x
)
=
{
1
n
αν
a
≤
x
≤
b
,
0
διαφορετικά
.
{\displaystyle p_{X}(x)={\begin{cases}{\frac {1}{n}}&{\text{αν }}a\leq x\leq b,\\0&{\text{διαφορετικά}}.\end{cases}}}
Από τον ορισμό της αναμενόμενης τιμής έχουμε ότι:
E
[
X
]
=
∑
x
=
a
b
1
n
⋅
x
=
1
n
⋅
(
b
⋅
(
b
+
1
)
2
−
a
⋅
(
a
−
1
)
2
)
=
1
n
⋅
(
b
2
−
a
2
+
b
+
a
2
)
=
1
n
⋅
(
(
b
−
a
)
⋅
(
b
+
a
+
1
)
2
)
=
1
n
⋅
(
(
b
−
a
+
1
)
⋅
(
b
+
a
)
2
)
=
(
b
+
a
)
2
,
{\displaystyle {\begin{aligned}\operatorname {E} [X]=\sum _{x=a}^{b}{\frac {1}{n}}\cdot x&={\frac {1}{n}}\cdot \left({\frac {b\cdot (b+1)}{2}}-{\frac {a\cdot (a-1)}{2}}\right)\\&={\frac {1}{n}}\cdot \left({\frac {b^{2}-a^{2}+b+a}{2}}\right)\\&={\frac {1}{n}}\cdot \left({\frac {(b-a)\cdot (b+a+1)}{2}}\right)\\&={\frac {1}{n}}\cdot \left({\frac {(b-a+1)\cdot (b+a)}{2}}\right)\\&={\frac {(b+a)}{2}},\end{aligned}}}
χρησιμοποιώντας ότι
∑
i
=
1
n
i
=
1
2
n
⋅
(
n
+
1
)
{\textstyle \sum _{i=1}^{n}i={\frac {1}{2}}n\cdot (n+1)}
Για να απλοποιήσουμε τον υπολογισμό της διακύμανσης , θα υπολογίσουμε την διακύμανση για την μεταβλητή
Y
=
X
−
a
+
1
{\displaystyle Y=X-a+1}
V
[
Y
]
=
V
[
X
−
a
+
1
]
=
V
[
X
]
,
{\displaystyle \operatorname {V} [Y]=\operatorname {V} [X-a+1]=\operatorname {V} [X],}
και τον ορισμό
V
[
Y
]
=
E
[
Y
2
]
−
(
E
[
Y
]
)
2
.
{\displaystyle \operatorname {V} [Y]=\operatorname {E} [Y^{2}]-(\operatorname {E} [Y])^{2}.}
Χρησιμοποιώντας τον ορισμό της αναμενόμενης τιμής, έχουμε ότι:
E
[
Y
2
]
=
∑
y
=
1
n
1
n
⋅
y
2
=
1
n
⋅
1
6
n
⋅
(
n
+
1
)
⋅
(
2
n
+
1
)
=
1
6
(
n
+
1
)
⋅
(
2
n
+
1
)
,
{\displaystyle \operatorname {E} [Y^{2}]=\sum _{y=1}^{n}{\frac {1}{n}}\cdot y^{2}={\frac {1}{n}}\cdot {\frac {1}{6}}n\cdot (n+1)\cdot (2n+1)={\frac {1}{6}}(n+1)\cdot (2n+1),}
χρησιμοποιώντας ότι
∑
i
=
1
n
i
2
=
1
6
n
⋅
(
n
+
1
)
⋅
(
2
n
+
1
)
{\textstyle \sum _{i=1}^{n}i^{2}={\frac {1}{6}}n\cdot (n+1)\cdot (2n+1)}
V
[
Y
]
=
1
6
(
n
+
1
)
⋅
(
2
n
+
1
)
−
1
4
(
n
+
1
)
2
=
n
+
1
2
⋅
n
−
1
4
=
n
2
−
1
12
.
{\displaystyle \operatorname {V} [Y]={\frac {1}{6}}(n+1)\cdot (2n+1)-{\frac {1}{4}}(n+1)^{2}={\frac {n+1}{2}}\cdot {\frac {n-1}{4}}={\frac {n^{2}-1}{12}}.}
Για
t
≠
1
{\displaystyle t\neq 1}
E
[
t
X
]
=
∑
x
=
a
b
1
n
⋅
t
x
=
1
n
⋅
t
b
−
t
a
t
−
1
,
{\displaystyle \operatorname {E} [t^{X}]=\sum _{x=a}^{b}{\frac {1}{n}}\cdot t^{x}={\frac {1}{n}}\cdot {\frac {t^{b}-t^{a}}{t-1}},}
χρησιμοποιώντας τον τύπο για το άθροισμα των όρων μίας γεωμετρικής προόδου .
Για
t
≠
0
{\displaystyle t\neq 0}
E
[
e
t
x
]
=
∑
x
=
a
b
1
n
⋅
e
t
x
=
1
n
⋅
e
t
b
−
e
t
a
e
t
−
1
,
{\displaystyle \operatorname {E} [e^{tx}]=\sum _{x=a}^{b}{\frac {1}{n}}\cdot e^{tx}={\frac {1}{n}}\cdot {\frac {e^{tb}-e^{ta}}{e^{t}-1}},}
χρησιμοποιώντας τον τύπο για το άθροισμα των όρων μίας γεωμετρικής προόδου .
Από τον ορισμό της εντροπίας , έχουμε ότι:
E
[
−
log
2
X
]
=
∑
x
=
a
b
−
1
n
⋅
log
2
(
1
n
)
=
−
n
⋅
1
n
⋅
log
2
(
1
n
)
=
log
2
n
.
{\displaystyle \operatorname {E} [-\log _{2}X]=\sum _{x=a}^{b}-{\frac {1}{n}}\cdot \log _{2}\left({\frac {1}{n}}\right)=-n\cdot {\frac {1}{n}}\cdot \log _{2}\left({\frac {1}{n}}\right)=\log _{2}n.}
Αυτή η κατανομή μεγιστοποιεί την εντροπία σε σχέση με όλες τις διακριτές κατανομές σε
n
{\displaystyle n}