Η γεωμετρική κατανομή είναι μια διακριτή συνάρτηση κατανομής τυχαίας μεταβλητής .
Περιγράφει το πλήθος πειραμάτων με δυο πιθανά αποτελέσματα (επιτυχία - αποτυχία) και πιθανότητα επιτυχίας
p
{\displaystyle p}
Παραδείγματα γεωμετρικής κατανομής με
p
=
0.2
,
0.35
,
0.5
{\displaystyle p=0.2,0.35,0.5}
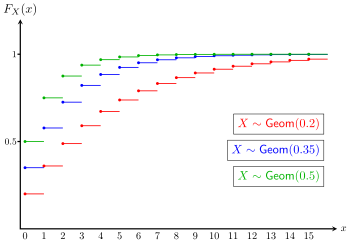
Παραδείγματα αθροιστικής κατανομής με
p
=
0.2
,
0.35
,
0.5
{\displaystyle p=0.2,0.35,0.5}
Γεωμετρική Κατανομή
Συμβολισμός
G
e
o
m
(
p
)
{\displaystyle {\mathsf {Geom}}(p)}
Παράμετροι
p
∈
[
0
,
1
]
{\displaystyle p\in [0,1]}
Φορέας
x
∈
{
1
,
2
,
…
}
{\displaystyle x\in \{1,2,\ldots \}}
Συνάρτηση Μάζας
p
⋅
(
1
−
p
)
x
−
1
{\displaystyle p\cdot (1-p)^{x-1}}
Μέσος
1
/
p
{\displaystyle 1/p}
Διάμεσος
⌈
−
1
log
2
(
1
−
p
)
⌉
{\displaystyle \left\lceil {\frac {-1}{\log _{2}(1-p)}}\right\rceil }
Διακύμανση
1
−
p
p
2
{\displaystyle {\frac {1-p}{p^{2}}}}
Λοξότητα
2
−
p
1
−
p
{\displaystyle {\frac {2-p}{\sqrt {1-p}}}}
Κύρτωση
3
+
p
2
1
−
p
{\displaystyle 3+{\frac {p^{2}}{1-p}}}
Εντροπία
−
log
2
p
−
1
−
p
p
⋅
log
2
(
1
−
p
)
{\displaystyle -\log _{2}p-{\frac {1-p}{p}}\cdot \log _{2}(1-p)}
Ροπή
E
[
X
k
]
=
p
{\displaystyle \operatorname {E} [X^{k}]=p}
Πιθανογεννήτρια
p
⋅
t
1
−
(
1
−
p
)
⋅
t
{\displaystyle {\frac {p\cdot t}{1-(1-p)\cdot t}}}
|
t
|
<
1
1
−
p
{\displaystyle |t|<{\frac {1}{1-p}}}
Χαρακτηριστική
p
⋅
e
t
1
−
(
1
−
p
)
⋅
e
t
{\displaystyle {\frac {p\cdot e^{t}}{1-(1-p)\cdot e^{t}}}}
e
t
<
1
1
−
p
{\displaystyle e^{t}<{\frac {1}{1-p}}}
Θεωρούμε την τυχαία μεταβλητή
X
{\displaystyle X}
x
∈
{
1
,
2
,
…
}
{\displaystyle x\in \{1,2,\ldots \}}
p
{\displaystyle p}
[ 1] [ 2] [ 3] [ 4] [ 5]
P
(
X
=
x
)
=
p
(
1
−
p
)
x
−
1
{\displaystyle \operatorname {P} (X=x)=p(1-p)^{x-1}}
Το πλήθος των φορών
X
{\displaystyle X}
G
e
o
m
(
1
/
2
)
{\displaystyle {\mathsf {Geom}}(1/2)}
Το πλήθος των φορών
X
{\displaystyle X}
G
e
o
m
(
1
/
1000
)
{\displaystyle {\mathsf {Geom}}(1/1000)}
1000
{\displaystyle 1000}
Αν ένας αλγόριθμος έχει πιθανότητα σφάλματος
ϵ
{\displaystyle \epsilon }
G
e
o
m
(
1
/
(
1
−
ϵ
)
)
{\displaystyle {\mathsf {Geom}}(1/(1-\epsilon ))}
Απόδειξη 1η: Θα χρησιμοποιήσουμε την εξής φόρμουλα για τον υπολογισμό της μέσης τιμής:
E
[
X
]
=
∑
x
=
1
∞
Pr
(
X
≥
x
)
.
{\displaystyle \operatorname {E} [X]=\sum _{x=1}^{\infty }\Pr(X\geq x).}
Η πιθανότητα να έρθει η πρώτη επιτυχία μετά το
x
{\displaystyle x}
x
−
1
{\displaystyle x-1}
P
(
X
≥
x
)
=
(
1
−
p
)
x
−
1
.
{\displaystyle \operatorname {P} (X\geq x)=(1-p)^{x-1}.}
επιστρέφοντας στον τύπο της μέσης τιμής, έχουμε ότι:
E
[
X
]
=
∑
x
=
1
∞
Pr
(
X
≥
x
)
=
∑
x
=
1
∞
(
1
−
p
)
x
−
1
=
∑
x
=
1
∞
(
1
−
p
)
x
=
1
1
−
(
1
−
p
)
=
1
p
.
{\displaystyle \operatorname {E} [X]=\sum _{x=1}^{\infty }\Pr(X\geq x)=\sum _{x=1}^{\infty }(1-p)^{x-1}=\sum _{x=1}^{\infty }(1-p)^{x}={\frac {1}{1-(1-p)}}={\frac {1}{p}}.}
Απόδειξη 2η: Ένας εναλλακτικός τρόπος για την εύρεση την μέσης τιμής είναι ο εξής:
E
[
X
]
=
∑
x
=
0
∞
x
⋅
p
⋅
(
1
−
p
)
x
−
1
=
∑
x
=
0
∞
p
⋅
(
x
⋅
(
1
−
p
)
x
−
1
)
=
∑
x
=
0
∞
p
⋅
d
d
p
(
−
(
1
−
p
)
x
)
=
p
⋅
d
d
p
(
−
∑
x
=
0
∞
(
1
−
p
)
x
)
=
p
⋅
d
d
p
(
−
1
p
)
=
p
⋅
1
p
2
=
1
p
.
{\displaystyle {\begin{aligned}\operatorname {E} [X]&=\sum _{x=0}^{\infty }x\cdot p\cdot (1-p)^{x-1}\\&=\sum _{x=0}^{\infty }p\cdot \left(x\cdot (1-p)^{x-1}\right)\\&=\sum _{x=0}^{\infty }p\cdot {\frac {d}{dp}}\left(-(1-p)^{x}\right)\\&=p\cdot {\frac {d}{dp}}\left(-\sum _{x=0}^{\infty }(1-p)^{x}\right)\\&=p\cdot {\frac {d}{dp}}\left(-{\frac {1}{p}}\right)\\&=p\cdot {\frac {1}{p^{2}}}\\&={\frac {1}{p}}.\end{aligned}}}
Ξεκινάμε υπολογίζοντας την τιμή:
E
[
X
⋅
(
X
−
1
)
]
=
∑
x
=
0
∞
p
⋅
(
1
−
p
)
x
−
1
⋅
x
⋅
(
x
−
1
)
=
p
⋅
(
1
−
p
)
⋅
∑
x
=
2
∞
(
1
−
p
)
x
−
2
⋅
x
⋅
(
x
−
1
)
=
p
⋅
(
1
−
p
)
⋅
∑
x
=
2
∞
d
d
p
2
(
(
1
−
p
)
x
)
=
p
⋅
(
1
−
p
)
⋅
d
2
d
p
2
∑
x
=
2
∞
(
1
−
p
)
x
=
p
⋅
(
1
−
p
)
⋅
d
2
d
p
2
(
1
−
p
)
2
p
=
p
⋅
(
1
−
p
)
⋅
d
d
p
(
1
−
1
p
2
)
=
p
⋅
(
1
−
p
)
⋅
2
p
3
=
2
⋅
1
−
p
p
2
.
{\displaystyle {\begin{aligned}\operatorname {E} [X\cdot (X-1)]&=\sum _{x=0}^{\infty }p\cdot (1-p)^{x-1}\cdot x\cdot (x-1)\\&=p\cdot (1-p)\cdot \sum _{x=2}^{\infty }(1-p)^{x-2}\cdot x\cdot (x-1)\\&=p\cdot (1-p)\cdot \sum _{x=2}^{\infty }{\frac {d}{dp^{2}}}\left((1-p)^{x}\right)\\&=p\cdot (1-p)\cdot {\frac {d^{2}}{dp^{2}}}\sum _{x=2}^{\infty }(1-p)^{x}\\&=p\cdot (1-p)\cdot {\frac {d^{2}}{dp^{2}}}{\frac {(1-p)^{2}}{p}}\\&=p\cdot (1-p)\cdot {\frac {d}{dp}}\left(1-{\frac {1}{p^{2}}}\right)\\&=p\cdot (1-p)\cdot {\frac {2}{p^{3}}}\\&=2\cdot {\frac {1-p}{p^{2}}}.\end{aligned}}}
Η διακύμανση τότε δίνεται από τον τύπο:
V
[
X
]
=
E
[
X
⋅
(
X
−
1
)
]
+
E
[
X
]
−
(
E
[
X
]
)
2
=
2
⋅
1
−
p
p
2
+
1
p
−
1
p
2
=
1
−
p
p
2
.
{\displaystyle {\begin{aligned}\operatorname {V} [X]&=\operatorname {E} [X\cdot (X-1)]+\operatorname {E} [X]-(\operatorname {E} [X])^{2}\\&=2\cdot {\frac {1-p}{p^{2}}}+{\frac {1}{p}}-{\frac {1}{p^{2}}}\\&={\frac {1-p}{p^{2}}}.\end{aligned}}}
Θέλουμε να βρούμε την μικρότερη τιμή του
x
{\displaystyle x}
P
(
X
≥
x
)
=
(
1
−
p
)
x
≤
1
2
.
{\displaystyle \operatorname {P} (X\geq x)=(1-p)^{x}\leq {\frac {1}{2}}.}
Ισοδύναμα,
x
log
2
(
1
−
p
)
≤
−
1.
{\displaystyle x\log _{2}(1-p)\leq -1.}
Δηλαδή,
x
=
⌈
−
1
log
2
(
1
−
p
)
⌉
.
{\displaystyle x=\left\lceil {\frac {-1}{\log _{2}(1-p)}}\right\rceil .}
Από τον ορισμό της εντροπίας , έχουμε ότι:
E
[
−
log
2
X
]
=
−
∑
x
=
0
∞
p
⋅
(
1
−
p
)
x
−
1
⋅
log
2
(
p
⋅
(
1
−
p
)
x
−
1
)
=
−
∑
x
=
0
∞
p
⋅
(
1
−
p
)
x
−
1
⋅
log
2
p
−
∑
x
=
0
∞
p
⋅
(
1
−
p
)
x
⋅
(
x
−
1
)
⋅
log
2
(
1
−
p
)
=
−
(
log
2
p
)
⋅
∑
x
=
0
∞
p
⋅
(
1
−
p
)
x
−
1
−
(
log
2
(
1
−
p
)
)
⋅
∑
x
=
2
∞
p
⋅
(
1
−
p
)
x
−
2
⋅
(
x
−
1
)
=
−
log
2
p
−
(
log
2
(
1
−
p
)
)
E
[
X
−
1
]
=
−
log
2
p
−
1
−
p
p
⋅
log
2
(
1
−
p
)
.
{\displaystyle {\begin{aligned}\operatorname {E} [-\log _{2}X]&=-\sum _{x=0}^{\infty }p\cdot (1-p)^{x-1}\cdot \log _{2}\left(p\cdot (1-p)^{x-1}\right)\\&=-\sum _{x=0}^{\infty }p\cdot (1-p)^{x-1}\cdot \log _{2}p-\sum _{x=0}^{\infty }p\cdot (1-p)^{x}\cdot (x-1)\cdot \log _{2}(1-p)\\&=-(\log _{2}p)\cdot \sum _{x=0}^{\infty }p\cdot (1-p)^{x-1}-(\log _{2}(1-p))\cdot \sum _{x=2}^{\infty }p\cdot (1-p)^{x-2}\cdot (x-1)\\&=-\log _{2}p-(\log _{2}(1-p))\operatorname {E} [X-1]\\&=-\log _{2}p-{\frac {1-p}{p}}\cdot \log _{2}(1-p).\end{aligned}}}
Από τον ορισμό της πιθανογεννήτριας συνάρτησης , έχουμε ότι:
E
[
t
X
]
=
∑
x
=
0
∞
p
⋅
(
1
−
p
)
x
−
1
⋅
t
x
=
p
⋅
t
⋅
∑
x
=
0
∞
(
(
1
−
p
)
⋅
t
)
x
−
1
=
p
⋅
t
⋅
1
1
−
(
1
−
p
)
⋅
t
,
{\displaystyle {\begin{aligned}\operatorname {E} [t^{X}]&=\sum _{x=0}^{\infty }p\cdot (1-p)^{x-1}\cdot t^{x}\\&=p\cdot t\cdot \sum _{x=0}^{\infty }((1-p)\cdot t)^{x-1}\\&=p\cdot t\cdot {\frac {1}{1-(1-p)\cdot t}},\end{aligned}}}
χρησιμοποιώντας ότι
|
t
|
<
1
1
−
p
{\displaystyle |t|<{\frac {1}{1-p}}}
Από τον ορισμό της χαρακτηριστικής συνάρτησης , έχουμε ότι:
E
[
e
t
X
]
=
∑
x
=
0
∞
p
⋅
(
1
−
p
)
x
−
1
⋅
e
t
x
=
p
⋅
e
t
⋅
∑
x
=
0
∞
(
(
1
−
p
)
⋅
e
t
)
x
−
1
=
p
⋅
e
t
⋅
1
1
−
(
1
−
p
)
⋅
e
t
,
{\displaystyle {\begin{aligned}\operatorname {E} [e^{tX}]&=\sum _{x=0}^{\infty }p\cdot (1-p)^{x-1}\cdot e^{tx}\\&=p\cdot e^{t}\cdot \sum _{x=0}^{\infty }((1-p)\cdot e^{t})^{x-1}\\&=p\cdot e^{t}\cdot {\frac {1}{1-(1-p)\cdot e^{t}}},\end{aligned}}}
χρησιμοποιώντας ότι
e
t
<
1
1
−
p
{\displaystyle e^{t}<{\frac {1}{1-p}}}




![{\displaystyle p\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)








![{\displaystyle \operatorname {E} [X^{k}]=p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8de29c49d4daffb36744779158467fd991251f5)





