Αρχείο:Pi 30K.gif
Pi_30K.gif (500 × 500 εικονοστοιχεία, μέγεθος αρχείου: 476 KB, τύπος MIME: image/gif, κυκλικά επαναλαμβανόμενο, 10 καρέ, 2,0 s)
Ιστορικό αρχείου
Κλικάρετε σε μια ημερομηνία/ώρα για να δείτε το αρχείο όπως εμφανιζόταν εκείνη τη στιγμή.
| Ώρα/Ημερομ. | Μικρογραφία | Διαστάσεις | Χρήστης | Σχόλια | |
|---|---|---|---|---|---|
| τελευταία | 16:00, 16 Φεβρουαρίου 2017 |  | 500 × 500 (476 KB) | Nicoguaro | Make the plot square and increase gif delay. |
| 15:38, 16 Φεβρουαρίου 2017 |  | 640 × 480 (476 KB) | Nicoguaro | Bigger text in the axes, and colors from ColorBrewer. Code in Python. | |
| 18:29, 7 Νοεμβρίου 2011 |  | 500 × 500 (373 KB) | Rayhem | Slowed animation to avoid looking like a blinky page element, improved resolution, added counter for number of points, shaded points inside/outside the circle. ==Mathematica 7.0 Source== <pre> tinyColor[color_, point_] := {PointSize[Small], color, Point[ | |
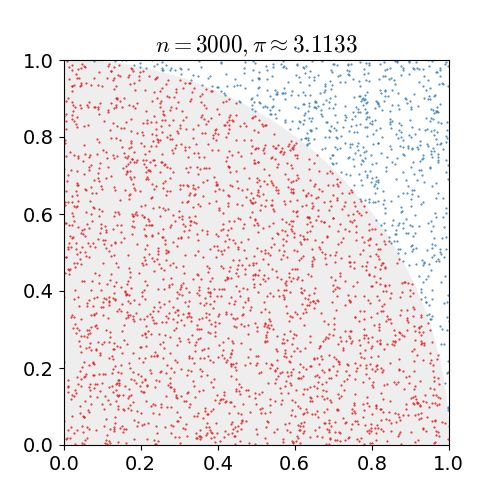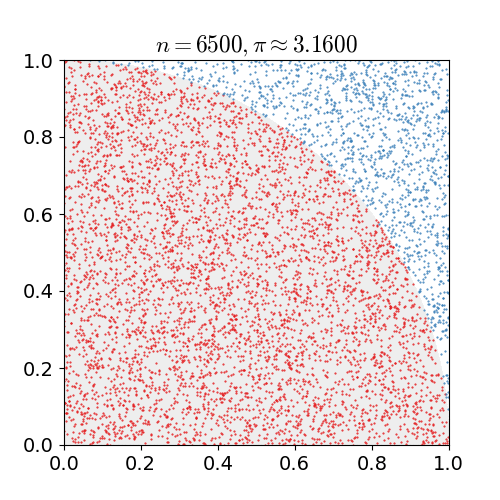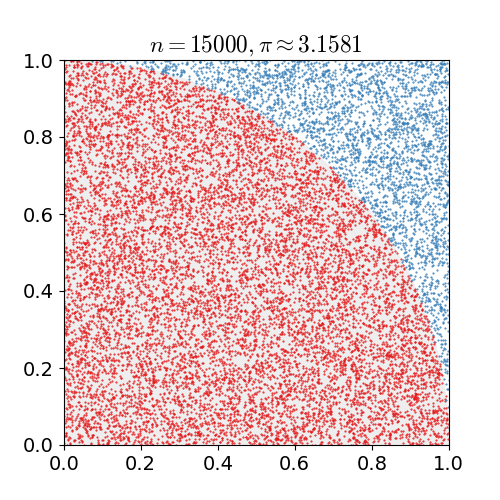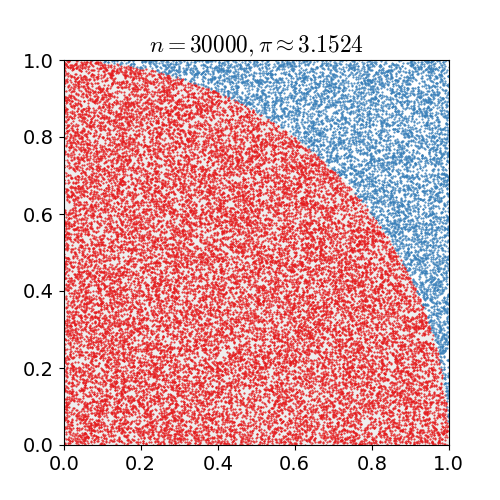
| 23:12, 14 Μαρτίου 2011 |  | 360 × 369 (363 KB) | CaitlinJo | {{Information |Description ={{en|1=As points are randomly scattered inside the unit square, some fall within the unit circle. The fraction of points inside the circle over all points approaches pi as the number of points goes toward infinity. This ani |
Συνδέσεις αρχείου
Τα παρακάτω λήμματα συνδέουν σε αυτό το αρχείο:
Καθολική χρήση αρχείου
Τα ακόλουθα άλλα wiki χρησιμοποιούν αυτό το αρχείο:
- Χρήση σε ar.wiki.x.io
- Χρήση σε be.wiki.x.io
- Χρήση σε bg.wiki.x.io
- Χρήση σε ca.wiki.x.io
- Χρήση σε da.wiki.x.io
- Χρήση σε en.wiki.x.io
- Χρήση σε en.wikibooks.org
- Χρήση σε eo.wiki.x.io
- Χρήση σε eu.wiki.x.io
- Χρήση σε fa.wiki.x.io
- Χρήση σε fr.wiki.x.io
- Χρήση σε he.wiki.x.io
- Χρήση σε hi.wiki.x.io
- Χρήση σε id.wiki.x.io
- Χρήση σε it.wiki.x.io
- Χρήση σε ja.wiki.x.io
- Χρήση σε ko.wiki.x.io
- Χρήση σε pt.wiki.x.io
- Χρήση σε sh.wiki.x.io
- Χρήση σε simple.wiki.x.io
- Χρήση σε sl.wiki.x.io
- Χρήση σε sr.wiki.x.io
- Χρήση σε sv.wiki.x.io
- Χρήση σε ta.wiki.x.io
- Χρήση σε test.wiki.x.io
- Χρήση σε th.wiki.x.io
- Χρήση σε tr.wiki.x.io
- Χρήση σε uk.wiki.x.io
- Χρήση σε vi.wiki.x.io
- Χρήση σε www.wikidata.org
- Χρήση σε zh-yue.wiki.x.io
- Χρήση σε zh.wiki.x.io